 西師大版五年級下冊數學第四單元4.3探索規律 教案.docx
西師大版五年級下冊數學第四單元4.3探索規律 教案.docx
4.3 探索規律 u 教學內容教材第69-70頁的“探索數列中各數之間的規律、運用圖形進行分數加法計算”,課堂活動及練習二十的內容。u 教材提示探索規律這一節內容是在學生學習掌握了分數加減混合運算順序以及會用加法的運算律和減法的性質進行簡便運算的基礎上進行教學的。本節內容主要包括2個例題、1個課堂活動和練習二十,通過本節課的學習,要使學生掌握:1.探究和掌握分數排列的一般規律。2。探究和掌握圖形表示分數的規律和技巧,讓學生感受圖形的變化規律。教學中,教師要注意引導學生觀察和分析,讓學生根據已知的數、圖,以小組的形式進行合理的推理,尋找問題的答案。加深對所學的數、圖形的規律的發現和理解。初步體會到數形結合的思想。為以后學習探索規律打下了基礎。u 教學目標知識與技能:經歷探索數列中各數之間的規律、運用圖形進行分數加法計算的過程,初步掌握探索規律的方法。能根據探索出的規律解決簡單的問題,提高學生分析問題、解決問題的能力。 過程與方法:通過觀察分析、合作交流,根據相鄰數字或圖形之間的關系,找出它們之間蘊涵的規律。情感、態度和價值觀:讓學生在探究中發現數之間和圖形之間的規律的過程中,發展學生的探究能力,培養學生愛數學的積極情感。u 重點、難點重點探索數之間、圖形和數之間蘊涵的規律。難點能根據探索出的規律解決問題。u 教學準備教師準備:課件、投影儀等。學生準備:正方形紙、鉛筆、直尺等。u 教學過程(一)新課導入:1舊知練習。找規律,在“?”處填幾?2.揭示課題。 通過上面的練習我們可以知識,掌握了規律,我們就可以輕松解決問題。今天,老師帶領大家一起去探索分數加減法中的有趣的規律問題。板書課題:探索規律設計意圖:通過舊知的練習,使學生體會到只有發現數字規律,就能輕松而有效地解決問題,培養了學生探索規律的興趣,同時也激起了學生的求知欲,為下一步的學習做好了心里準備。(二)探究新知:1.教學例1:課件出示第(1)題。(1)請同學們觀察這幾個分數,想一想,這幾個分數之間有什么規律?學生獨立觀察,尋找規律。小組交流。在小組里互相說一說自己發現的規律,糾正同伴錯誤的發現。反饋匯報。根據學生的匯報小結:這一組分數的分母依次是2,3,4,分子依次是1,2,3,也就是說,后一個分數的分子和分母都比前一個分數的分子和分母大1。(2)根據規律,完成填空。學生獨立填寫,教師巡視,對學困生給予指導。匯報展示。指名匯報,并在黑板上展示學生的學習成果。2.課件出示第(2)題。(1)請同學們再觀察這一組數,找一找,這一組數有什么規律?學生獨立觀察思考,尋找這一組數的規律。小組交流。在小組里說一說自己發現的規律,教師走到各小組,聽聽學生的發言。各小組選派代表反饋匯報:方法一:把分數化成小數,變成0.2,0.4,0.6,0.8,后一個數都比前一個數多0.2。方法二:把小數化成分數,變成,后一個分數都比前一個分數多。方法三:分數和小數交叉排列的,后一個分數比前一個分數多,后一個小數比前一個小數多0.4。(2)要求學生根據規律,完成填空。學生根據發現的規律,獨立完成填空。教師巡視,對學困生給予指導。匯報展示。指名匯報,展示學生的填寫結果。設計意圖:讓學生探索數的排列規律,并能根據規律完成填空。使學生在探究中掌握尋找一組數規律的方法,同時體會尋找一組數規律方法的多樣性。3.教學例2:課件出示例2第(1)小題:+ (1) 提問:如何在一張紙上表示出+ ?試一試。操作:拿出準備好的正方形紙,把紙平均分成2份,把涂上顏色,在沒有涂色的部分找出一張紙的,把這也涂上顏色。(2)思考:涂色的部分與沒有涂色的部分有什么關系?學生回答:涂色的部分和沒有涂色的部分合起來就是一張紙的大小;涂色的部分等于整張正方形紙去掉沒有涂色的部分。(3)啟發:如果把這張正方形紙看作單位“1”,沒有涂色的部分是這張正方形紙的幾分之幾?涂色的部分除了可以寫成“+ ”,還可以怎樣寫?學生思考、交流后,反饋匯報。根據學生的匯報小結:如果把這張正方形紙看作單位“1”,沒有涂色的部分是這張紙的,所以涂色的部分還可以寫成1- 。(4)根據涂色部分與沒有涂色部分的關系,計算+ 的和。引導學生根據規律寫出算式:+ =1- = 。4.課件出示例2第(2)題:+ + (1)操作:再拿出一張準備好的正方形紙,把紙平均分成2份,把涂上色,在沒有涂色的部分找出一張紙的,把這也涂上色;然后余下的沒有涂色的部分找出,把這也涂上色。(2)思考:沒有涂色的部分占整張紙的幾分之幾?它們有什么關系?學生回答:沒有涂色部分占整張紙的,涂色部分和沒有涂色部分加起來就是一張紙的大小。(3)啟發:觀察涂色后的正方形紙,想一想:如果把整張紙看作單位“1”,“ + + ”除用通分相加的方法,還可以用什么方法計算?學生思考、交流后,匯報。匯報小結:如果把這張正方形紙看作單位“1”,沒有涂色的部分是這張紙的,所以涂色的部分還可以用“1- ”來計算。(4)學生用探索出來的方法,獨立計算“+ + ”,舉手匯報結果。5.自主探索:課件出示第(3)小題和第(4)小題。(1)提示要求:用探索第(1)小題和第(2)小題同樣的方法,自主探索第(3)和第(4)小題的規律。(2)學生自主探索,教師巡視,對學困生給予幫助。(3)小組交流。每位同學在小組里說說自己的探索過程和找到的規律。(4)反饋匯報:第(3)題:“+ + + ”所對應的圖中,沒有涂色的部分占,所以+ + =1- = 。第(4)題:“+ + + + ”所對應的圖中,沒有涂色的部分占,所以+ + + =1- = 。6.嘗試練習。課件出示69頁“試一試”。(1)請同學們獨立探索,用涂色的方法求出這個分數加法算式的值。(2)學生自主探索,教師巡視。(3)小組交流。學生在小組里說一說自己的探索方法和求得的結果。(4)指名匯報。根據學生的匯報小結:+ + + + + =1- = 。設計意圖:以學生為主體,讓學生通過動手操作、自主探索,引導學生從不同的角度思考問題,探究出問題中的規律,找出解決問題的方法。7.教學“課堂活動”課件出示“課堂活動”主題圖。(1)請同學們根據剛才探究問題的方法,想一想,這幾幅圖有什么規律?(2)學生思考分析四幅圖的規律,并在小組里和同學交流自己的看法。(3)小組選派代表匯報。(4)師生共同總結規律:每個圖形陰影部分的面積都是所分成的每份數面積的一半。設計意圖:通過探索陰影部分的面積,讓學生再次經歷探索規律的過程,進一步提高學生的觀察能力和分析能力。(三)鞏固新知:1.完成70頁“練習二十”第1題。(1)學生根據解決例題過程中所用的方法,自主探索每小題的規律。(2)小組交流。在小組里互相說一說自己發現的規律以及理由。(3)反饋匯報。2.完成70頁“練習二十”第2題。(1)學生自主探索規律,完成填空。(2)指名全班匯報:后一個圖形的陰影部分都是前一個圖形陰影部分的。(四)達標反饋習題;1.先找規律,再在括號里填上合適的數。,0.6,0.8,( ),( ),( ),( )2.察下面算式的計算過程,尋找規律后再計算。+ = + = 3.尋找算式的規律,直接寫出得數。-= -= -=答案:1. 2. 3.,(五)課堂小結說一說這一節課有什么收獲?學生匯報小結:1.發現了一組分數,可以分析分子、分母的變化規律,如分子、分母增加了多少或減少了多少,從而發現分數的排列規律。2.對于分數與小數交叉排列的一組數,可以把分數化成小數或把小數化成分數來尋找規律,也可以間隔著尋找分數的排列規律和小數的排列規律。3.對于有規律的分數加法,可以用畫圖涂色的方法,根據沒有涂色部分面積占幾分之幾,用減法求出涂色部分的面積。設計意圖:通過讓學生按課堂教學的順序進行回憶總結,使學生再一次復習和鞏固了所學的知識,更加充分和靈活地掌握了知識。(六)布置作業1.完成練習二十的第3題。2.課后同位合作,按書中所學的內容,互相考查。3.找規律,用分數表示陰影部分的面積。( ) ( )4.找規律計算。答案:3. 4. u 板書設計 3探索規律1一列分數:尋找前后分數分子、分母的關系。2分數、小數交叉混合:尋找分數與分數之間、小數與小數之間的規律。把分數化成小數,再尋找小數列的規律。把小數化成分數,再尋找分數列的規律。3.有規律的分數加法:把一個正方形看作單位“1”,在正方形里依次涂出表示各個分數的部分,用單位“1”減去沒有涂色部分占正方形的幾分之幾,就得到幾個分數的和是多少。u 教學反思本節課是規律探索課,所以本節課要體現在探索的環節上,由此出發,本節課有以下特點:1、 讓學生充分自主探索、合作交流,盡量發揮學生的能動性。對于例題中每一條規律的認識過程中,都注重讓學生思考、分析、交流,學生在生生互動、師生互動的過程中,發現規律,掌握尋找規律的方法。2、 注重轉化思想的運用,培養學生逆向思維能力。在例2的教學過程中,充分利用正方形紙涂色后,分析涂色部分與未涂色部分的關系,讓學生明確分數加法的結果可以用單位1減去未涂色部分所占的幾分之幾,把本來的加法算式轉化成減法算式來進行計算。這樣,省略了繁瑣的通分過程,使本來較復雜的分數加法計算變得簡單、易解。教學資源:答案:知識鏈接:數字找規律的方法第一種等差數列:是指相鄰之間的差值相等,整個數字序列依次遞增或遞減的一組數。如:1,3,5,7,9相鄰兩數之間的差都相等。在分數中還有一種分子分母的等差數列,主要表現在分數中,分子或分母、分子和分母分別呈現等差數列的規律性。如:,第二種混合數列式:是兩個數列交替排列在一列數中,有時是兩個相同的數列(等差或等比),有時兩個數列是按不同規律排列的。如:26,11,31,6,36,1這一組數中,奇數項按加5遞增,偶數項按減5遞減;第四種四則混合運算:是指前兩(或幾)個數經過某種四則運算等到于下一個數,如前兩個數之和、之差、之積、之商等于第三個數。如:2,4,6,10,16,26這一組數中,從第三個數開始,分別是前兩個數之和。數字的排列規律還有很多,需要我們仔細分析,才能正常找出數字排列的規律
- 關 鍵 詞:
- 西師大版五年級下冊數學第四單元4.3探索規律 教案 師大 年級 下冊 數學 第四 單元 4.3 探索 規律
 叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。
叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。 關于本文



 24秋新一年級上冊語文2 江南(朗讀音頻).mp3
24秋新一年級上冊語文2 江南(朗讀音頻).mp3  人民版初中《中華民族大團結》第05課 共同保衛偉大祖國 課件.ppt
人民版初中《中華民族大團結》第05課 共同保衛偉大祖國 課件.ppt  人民版初中《中華民族大團結》第04課 共同開發建設祖國 課件.pptx
人民版初中《中華民族大團結》第04課 共同開發建設祖國 課件.pptx  人民版初中《中華民族大團結》第11課 團結奮斗繁榮發展 課件.pptx
人民版初中《中華民族大團結》第11課 團結奮斗繁榮發展 課件.pptx  人民版初中《中華民族大團結》第08課 共同繁榮文學藝術 課件.pptx
人民版初中《中華民族大團結》第08課 共同繁榮文學藝術 課件.pptx  人民版初中《中華民族大團結》第07課 共同創造科學成就 課件.ppt
人民版初中《中華民族大團結》第07課 共同創造科學成就 課件.ppt  人民版初中《中華民族大團結》第10課 偉大夢想 共同追求 課件.pptx
人民版初中《中華民族大團結》第10課 偉大夢想 共同追求 課件.pptx  人民版初中《中華民族大團結》第06課 共同筑牢民族團結基石 課件.pptx
人民版初中《中華民族大團結》第06課 共同筑牢民族團結基石 課件.pptx  人民版初中《中華民族大團結》第02課 中華民族的形成發展 課件.ppt
人民版初中《中華民族大團結》第02課 中華民族的形成發展 課件.ppt  人民版初中《中華民族大團結》第09課 共同弘揚中華傳統美德 課件.pptx
人民版初中《中華民族大團結》第09課 共同弘揚中華傳統美德 課件.pptx  人民版初中《中華民族大團結》第01課 愛我中華 課件.pptx
人民版初中《中華民族大團結》第01課 愛我中華 課件.pptx  人民版初中《中華民族大團結》第03課 中華民族精神 課件.pptx
人民版初中《中華民族大團結》第03課 中華民族精神 課件.pptx  人民版初中《中華民族大團結》第12課 黨的領導根本保證 課件.ppt
人民版初中《中華民族大團結》第12課 黨的領導根本保證 課件.ppt  人民版初中《中華民族大團結》教學課件ppt(全冊打包下載).rar
人民版初中《中華民族大團結》教學課件ppt(全冊打包下載).rar 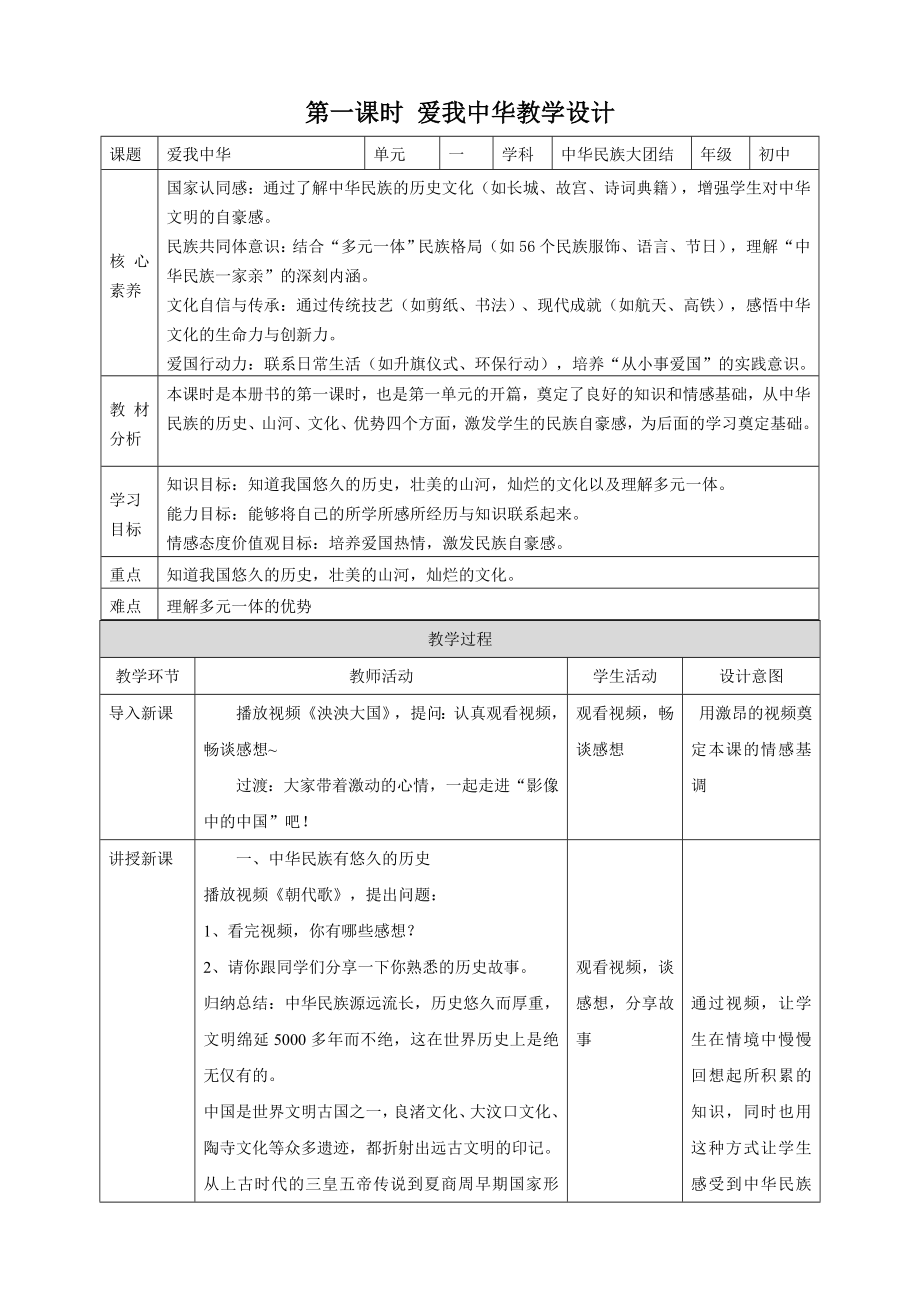 人民版初中《中華民族大團結》核心素養教案(全冊教學設計打包).rar
人民版初中《中華民族大團結》核心素養教案(全冊教學設計打包).rar 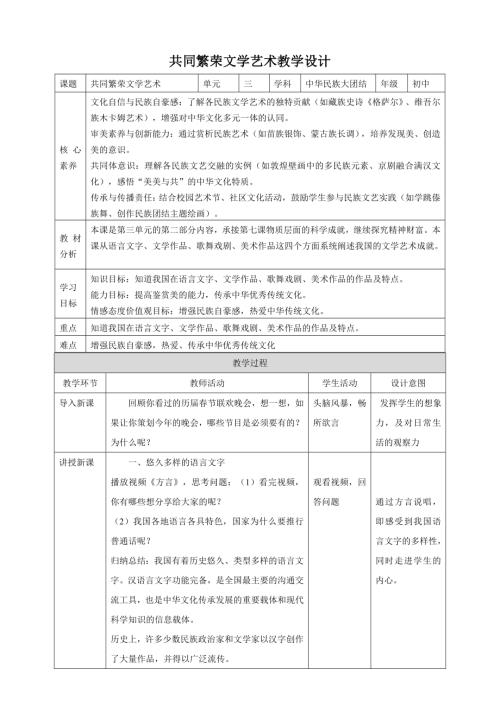 人民版初中《中華民族大團結》3.8 共同繁榮文學藝術 核心素養教案.doc
人民版初中《中華民族大團結》3.8 共同繁榮文學藝術 核心素養教案.doc 


