 2019年山西省中考數學試卷.doc
2019年山西省中考數學試卷.doc
2019年山西省中考數學試卷一、選擇題(本大題共10個小題,每小題3分,共30分,在每個小題給出的四個選項中,只有一項符合題目要求,請選出并在答題卡上將該項涂黑1(3分)3的絕對值是()A3B3CD2(3分)下列運算正確的是()A2a+3a5a2B(a+2b)2a2+4b2Ca2a3a6D(ab2)3a3b63(3分)某正方體的每個面上都有一個漢字,如圖是它的一種展開圖,那么在原正方體中,與“點”字所在面相對面上的漢字是()A青B春C夢D想4(3分)下列二次根式是最簡二次根式的是()ABCD5(3分)如圖,在ABC中,ABAC,A30,直線ab,頂點C在直線b上,直線a交AB于點D,交AC與點E,若1145,則2的度數是()A30B35C40D456(3分)不等式組的解集是()Ax4Bx1C1x4Dx17(3分)五臺山景區空氣清爽,景色宜人“五一”小長假期間購票進山游客12萬人次,再創歷史新高五臺山景區門票價格旺季168元/人以此計算,“五一”小長假期間五臺山景區進山門票總收入用科學記數法表示()A2.016108元B0.2016107元C2.016107元D2016104元8(3分)一元二次方程x24x10配方后可化為()A(x+2)23B( x+2)25C(x2)23D( x2)259(3分)北中環橋是省城太原的一座跨汾河大橋(如圖1),它由五個高度不同,跨徑也不同的拋物線型鋼拱通過吊橋,拉索與主梁相連,最高的鋼拱如圖2所示,此鋼拱(近似看成二次函數的圖象拋物線)在同一豎直平面內,與拱腳所在的水平面相交于A,B兩點拱高為78米(即最高點O到AB的距離為78米),跨徑為90米(即AB90米),以最高點O為坐標原點,以平行于AB的直線為x軸建立平面直角坐標系,則此拋物線鋼拱的函數表達式為()Ayx2Byx2Cyx2Dyx210(3分)如圖,在RtABC中,ABC90,AB2,BC2,以AB的中點O為圓心,OA的長為半徑作半圓交AC于點D,則圖中陰影部分的面積為()AB+C2D4二、填空題(本大題共5個小題,每小題3分,共15分)11(3分)化簡的結果是 12(3分)要表示一個家庭一年用于“教育”,“服裝”,“食品”,“其他”這四項的支出各占家庭本年總支出的百分比,從“扇形統計圖”,“條形統計圖”,“折線統計圖”中選擇一種統計圖,最適合的統計圖是 13(3分)如圖,在一塊長12m,寬8m的矩形空地上,修建同樣寬的兩條互相垂直的道路(兩條道路各與矩形的一條平行),剩余部分栽種花草,且栽種花草的面積77m2,設道路的寬為xm,則根據題意,可列方程為 14(3分)如圖,在平面直角坐標中,點O為坐標原點,菱形ABCD的頂點B在x軸的正半軸上,點A坐標為(4,0),點D的坐標為(1,4),反比例函數y(x0)的圖象恰好經過點C,則k的值為 15(3分)如圖,在ABC中,BAC90,ABAC10cm,點D為ABC內一點,BAD15,AD6cm,連接BD,將ABD繞點A按逆時針方向旋轉,使AB與AC重合,點D的對應點為點E,連接DE,DE交AC于點F,則CF的長為 cm三、解答題(本大題共8個小題,共75分,解答應寫出文字說明,證明過程或演算步驟)16(10分)(1)計算:+()23tan60+()0(2)解方程組:17(7分)已知:如圖,點B,D在線段AE上,ADBE,ACEF,CF求證:BCDF18(9分)中華人民共和國第二屆青年運動會(簡稱二青會)將于2019年8月在山西舉行太原市作為主賽區,將承擔多項賽事,現正從某高校的甲、乙兩班分別招募10人作為頒獎禮儀志愿者,同學們踴躍報名,甲、乙兩班各報了20人,現已對他們進行了基本素質測評,滿分10分各班按測評成績從高分到低分的順序各錄用10人,對這次基本素質測評中甲、乙兩班學生的成績繪制了如圖所示的統計圖請解答下列問題:(1)甲班的小華和乙班的小麗基本素質測評成績都為7分,請你分別判斷小華,小麗能否被錄用(只寫判斷結果,不必寫理由)(2)請你對甲、乙兩班各被錄用的10名志愿者的成績作出評價(從“眾數”,“中位數”,或“平均數”中的一個方面評價即可)(3)甲、乙兩班被錄用的每一位志愿者都將通過抽取卡片的方式決定去以下四個場館中的兩個場館進行頒獎禮儀服務,四個場館分別為:太原學院足球場,太原市沙灘排球場,山西省射擊射箭訓練基地,太原水上運動中心,這四個場館分別用字母A,B,C,D表示現把分別印有A,B,C,D的四張卡片(除字母外,其余都相同)背面朝上,洗勻放好志愿者小玲從中隨機抽取一張(不放回),再從中隨機抽取一張,請你用列表或畫樹狀圖的方法求小玲抽到的兩張卡片恰好是“A”和“B”的概率19(8分)某游泳館推出了兩種收費方式方式一:顧客先購買會員卡,每張會員卡200元,僅限本人一年內使用,憑卡游泳,每次游泳再付費30元方式二:顧客不購買會員卡,每次游泳付費40元設小亮在一年內來此游泳館的次數為x次,選擇方式一的總費用為y1(元),選擇方式二的總費用為y2(元)(1)請分別寫出y1,y2與x之間的函數表達式(2)小亮一年內在此游泳館游泳的次數x在什么范圍時,選擇方式一比方式二省錢20(9分)某“綜合與實踐”小組開展了測量本校旗桿高度的實踐活動他們制訂了測量方案,并利用課余時間完成了實地測量他們在該旗桿底部所在的平地上,選取兩個不同測點,分別測量了該旗桿頂端的仰角以及這兩個測點之間的距離為了減小測量誤差,小組在測量仰角的度數以及兩個測點之間的距離時,都分別測量了兩次并取它們的平均值作為測量結果,測量數據如下表(不完整) 課題測量旗桿的高度成員組長:xxx 組員:xxx,xxx,xxx測量工具測量角度的儀器,皮尺等測量示意圖說明:線段GH表示學校旗桿,測量角度的儀器的高度ACBD1.5m,測點A,B與H在同一條水平直線上,A,B之間的距離可以直接測得,且點G,H,A,B,C,D都在同一豎直平面內,點C,D,E在同一條直線上,點E在GH 上測量數據測量項目第一次第二次平均值GCE的度數25.625.825.7GDE的度數31.230.831A,B之間的距離5.4m5.6m任務一:兩次測量A,B之間的距離的平均值是 m任務二:根據以上測量結果,請你幫助該“綜合與實踐”小組求出學校旗桿GH的高度(參考數據:sin25.70.43,cos25.70.90,tan25.70.48,sin310.52,cos310.86,tan310.60)任務三:該“綜合與實踐”小組在制定方案時,討論過“利用物體在陽光下的影子測量旗桿的高度”的方案,但未被采納你認為其原因可能是什么?(寫出一條即可)21(8分)閱讀以下材料,并按要求完成相應的任務:萊昂哈德歐拉(LeonhardEuler)是瑞士數學家,在數學上經常見到以他的名字命名的重要常數,公式和定理,下面就是歐拉發現的一個定理:在ABC中,R和r分別為外接圓和內切圓的半徑,O和I分別為其中外心和內心,則OI2R22Rr如圖1,O和I分別是ABC的外接圓和內切圓,I與AB相切分于點F,設O的半徑為R,I的半徑為r,外心O(三角形三邊垂直平分線的交點)與內心I(三角形三條角平分線的交點)之間的距離OId,則有d2R22Rr下面是該定理的證明過程(部分):延長AI交O于點D,過點I作O的直徑MN,連接DM,ANDN,DMINAI(同弧所對的圓周角相等)MDIANI,IAIDIMIN,如圖2,在圖1(隱去MD,AN)的基礎上作O的直徑DE,連接BE,BD,BI,IFDE是O的直徑,所以DBE90I與AB相切于點F,所以AFI90,DBEIFABADE(同弧所對的圓周角相等),AIFEDB,IABDDEIF任務:(1)觀察發現:IMR+d,IN (用含R,d的代數式表示);(2)請判斷BD和ID的數量關系,并說明理由(3)請觀察式子和式子,并利用任務(1),(2)的結論,按照上面的證明思路,完成該定理證明的剩余部分;(4)應用:若ABC的外接圓的半徑為5cm,內切圓的半徑為2cm,則ABC的外心與內心之間的距離為 cm22(11分)綜合與實踐動手操作:第一步:如圖1,正方形紙片ABCD沿對角線AC所在的直線折疊,展開鋪平在沿過點C的直線折疊,使點B,點D都落在對角線AC上此時,點B與點D重合,記為點N,且點E,點N,點F三點在同一條直線上,折痕分別為CE,CF如圖2第二步:再沿AC所在的直線折疊,ACE與ACF重合,得到圖3第三步:在圖3的基礎上繼續折疊,使點C與點F重合,如圖4,展開鋪平,連接EF,FG,GM,ME如圖5,圖中的虛線為折痕問題解決:(1)在圖5中,BEC的度數是 ,的值是 (2)在圖5中,請判斷四邊形EMGF的形狀,并說明理由;(3)在不增加字母的條件下,請你以圖中5中的字母表示的點為頂點,動手畫出一個菱形(正方形除外),并寫出這個菱形: 23(13分)綜合與探究如圖,拋物線yax2+bx+6經過點A(2,0),B(4,0)兩點,與y軸交于點C,點D是拋物線上一個動點,設點D的橫坐標為m(1m4)連接AC,BC,DB,DC(1)求拋物線的函數表達式;(2)BCD的面積等于AOC的面積的時,求m的值;(3)在(2)的條件下,若點M是x軸上一動點,點N是拋物線上一動點,試判斷是否存在這樣的點M,使得以點B,D,M,N為頂點的四邊形是平行四邊形?若存在,請直接寫出點M的坐標;若不存在,請說明理由2019年山西省中考數學試卷參考答案與試題解析一、選擇題(本大題共10個小題,每小題3分,共30分,在每個小題給出的四個選項中,只有一項符合題目要求,請選出并在答題卡上將該項涂黑1(3分)3的絕對值是()A3B3CD【考點】15:絕對值菁優網版權所有【分析】根據絕對值的定義,3的絕對值是指在數軸上表示3的點到原點的距離,即可得到正確答案【解答】解:|3|3故3的絕對值是3故選:B【點評】本題考查的是絕對值的定義,抓住定義及相關知識點即可解決問題2(3分)下列運算正確的是()A2a+3a5a2B(a+2b)2a2+4b2Ca2a3a6D(ab2)3a3b6【考點】35:合并同類項;46:同底數冪的乘法;47:冪的乘方與積的乘方;4C:完全平方公式菁優網版權所有【分析】直接利用合并同類項法則以及完全平方公式、積的乘方運算法則、同底數冪的乘除運算法則分別化簡得出答案【解答】解:A、2a+3a5a,故此選項錯誤;B、(a+2b)2a2+4ab+4b2,故此選項錯誤;C、a2a3a5,故此選項錯誤;D、(ab2)3a3b6,正確故選:D【點評】此題主要考查了合并同類項以及完全平方公式、積的乘方運算、同底數冪的乘除運算,正確掌握相關運算法則是解題關鍵3(3分)某正方體的每個面上都有一個漢字,如圖是它的一種展開圖,那么在原正方體中,與“點”字所在面相對面上的漢字是()A青B春C夢D想【考點】I8:專題:正方體相對兩個面上的文字菁優網版權所有【分析】根據正方體展開z字型和L型找對面的方法即可求解;【解答】解:展開圖中“點”與“春”是對面,“亮”與“想”是對面,“青”與“夢”是對面;故選:B【點評】本題考查正方體的展開圖;熟練掌握正方體展開圖找對面的方法是解題的關鍵4(3分)下列二次根式是最簡二次根式的是()ABCD【考點】74:最簡二次根式菁優網版權所有【分析】檢查最簡二次根式的兩個條件是否同時滿足,同時滿足的就是最簡二次根式,否則就不是【解答】解:解:A、,故A不符合題意;B、,故B不符合題意;C、,故C不符合題意;D、是最簡二次根式,故D符合題意故選:D【點評】本題考查最簡二次根式的定義,最簡二次根式必須滿足兩個條件:被開方數不含分母;被開方數不含能開得盡方的因數或因式5(3分)如圖,在ABC中,ABAC,A30,直線ab,頂點C在直線b上,直線a交AB于點D,交AC與點E,若1145,則2的度數是()A30B35C40D45【考點】JA:平行線的性質;KH:等腰三角形的性質菁優網版權所有【分析】先根據等腰三角形的性質和三角形的內角和可得ACB75,由三角形外角的性質可得AED的度數,由平行線的性質可得同位角相等,可得結論【解答】解:ABAC,且A30,ACB75,在ADE中,1A+AED145,AED14530115,ab,AED2+ACB,21157540,故選:C【點評】本題主要考查了等腰三角形的性質,平行線的性質,題目比較基礎,熟練掌握性質是解題的關鍵6(3分)不等式組的解集是()Ax4Bx1C1x4Dx1【考點】CB:解一元一次不等式組菁優網版權所有【分析】首先求出不等式組中每一個不等式的解集,再求出其公共解集【解答】解:,由得:x4,由得:x1,不等式組的解集為:x4,故選:A【點評】此題主要考查了解一元一次不等式組,關鍵是掌握解集的規律:同大取大;同小取小;大小小大中間找;大大小小找不到7(3分)五臺山景區空氣清爽,景色宜人“五一”小長假期間購票進山游客12萬人次,再創歷史新高五臺山景區門票價格旺季168元/人以此計算,“五一”小長假期間五臺山景區進山門票總收入用科學記數法表示()A2.016108元B0.2016107元C2.016107元D2016104元【考點】1I:科學記數法表示較大的數菁優網版權所有【分析】科學記數法就是將一個數字表示成(a10的n次冪的形式),其中1|a|10,n表示整數,即從左邊第一位開始,在首位非零的后面加上小數點,再乘以10的n次冪【解答】解:120000168201600002.016107,故選:C【點評】此題考查了對科學記數法的理解和運用和單位的換算科學記數法的表示形式為a10n的形式,其中1|a|10,n為整數,表示時關鍵要正確確定a的值以及n的值8(3分)一元二次方程x24x10配方后可化為()A(x+2)23B( x+2)25C(x2)23D( x2)25【考點】A6:解一元二次方程配方法菁優網版權所有【分析】移項,配方,即可得出選項【解答】解:x24x10,x24x1,x24x+41+4,(x2)25,故選:D【點評】本題考查了解一元二次方程的應用,能正確配方是解此題的關鍵9(3分)北中環橋是省城太原的一座跨汾河大橋(如圖1),它由五個高度不同,跨徑也不同的拋物線型鋼拱通過吊橋,拉索與主梁相連,最高的鋼拱如圖2所示,此鋼拱(近似看成二次函數的圖象拋物線)在同一豎直平面內,與拱腳所在的水平面相交于A,B兩點拱高為78米(即最高點O到AB的距離為78米),跨徑為90米(即AB90米),以最高點O為坐標原點,以平行于AB的直線為x軸建立平面直角坐標系,則此拋物線鋼拱的函數表達式為()Ayx2Byx2Cyx2Dyx2【考點】HD:根據實際問題列二次函數關系式菁優網版權所有【分析】直接利用圖象假設出拋物線解析式,進而得出答案【解答】解:設拋物線的解析式為:yax2,將B(45,78)代入得:78a452,解得:a,故此拋物線鋼拱的函數表達式為:yx2故選:B【點評】此題主要考查了根據實際問題列二次函數解析式,正確假設出拋物線解析式是解題關鍵10(3分)如圖,在RtABC中,ABC90,AB2,BC2,以AB的中點O為圓心,OA的長為半徑作半圓交AC于點D,則圖中陰影部分的面積為()AB+C2D4【考點】KQ:勾股定理;MO:扇形面積的計算菁優網版權所有【分析】根據題意,作出合適的輔助線,即可求得DE的長、DOB的度數,然后根據圖形可知陰影部分的面積是ABC的面積減去AOD的面積和扇形BOD的面積,從而可以解答本題【解答】解:在RtABC中,ABC90,AB2,BC2,tanA,A30,DOB60,ODAB,DE,陰影部分的面積是:,故選:A【點評】本題考查扇形面積的計算、勾股定理,解答本題的關鍵是明確題意,利用數形結合的思想解答二、填空題(本大題共5個小題,每小題3分,共15分)11(3分)化簡的結果是【考點】6B:分式的加減法菁優網版權所有【分析】先把異分母轉化成同分母,再把分子相減即可【解答】解:原式故答案為:【點評】此題考查了分式的加減運算,在分式的加減運算中,如果是同分母分式,那么分母不變,把分子直接相加減即可;如果是異分母分式,則必須先通分,把異分母分式化為同分母分式,然后再相加減12(3分)要表示一個家庭一年用于“教育”,“服裝”,“食品”,“其他”這四項的支出各占家庭本年總支出的百分比,從“扇形統計圖”,“條形統計圖”,“折線統計圖”中選擇一種統計圖,最適合的統計圖是扇形統計圖【考點】VE:統計圖的選擇菁優網版權所有【分析】條形統計圖能很容易看出數量的多少;折線統計圖不僅容易看出數量的多少,而且能反映數量的增減變化情況;扇形統計圖能反映部分與整體的關系;由此根據情況選擇即可【解答】解:要表示一個家庭一年用于“教育”,“服裝”,“食品”,“其他”這四項的支出各占家庭本年總支出的百分比,最適合的統計圖是扇形統計圖故答案為:扇形統計圖【點評】此題應根據條形統計圖、折線統計圖、扇形統計圖各自的特點進行解答13(3分)如圖,在一塊長12m,寬8m的矩形空地上,修建同樣寬的兩條互相垂直的道路(兩條道路各與矩形的一條平行),剩余部分栽種花草,且栽種花草的面積77m2,設道路的寬為xm,則根據題意,可列方程為(12x)(8x)77【考點】AC:由實際問題抽象出一元二次方程菁優網版權所有【分析】把所修的兩條道路分別平移到矩形的最上邊和最左邊,則剩下的草坪是一個長方形,根據長方形的面積公式列方程【解答】解:道路的寬應為x米,由題意得,(12x)(8x)77,故答案為:(12x)(8x)77【點評】此題主要考查了由實際問題抽象出一元二次方程,把中間修建的兩條道路分別平移到矩形地面的最上邊和最左邊是做本題的關鍵14(3分)如圖,在平面直角坐標中,點O為坐標原點,菱形ABCD的頂點B在x軸的正半軸上,點A坐標為(4,0),點D的坐標為(1,4),反比例函數y(x0)的圖象恰好經過點C,則k的值為16【考點】G4:反比例函數的性質;G6:反比例函數圖象上點的坐標特征;L8:菱形的性質菁優網版權所有【分析】要求k的值,求出點C坐標即可,由菱形的性質,再構造直角三角形,利用勾股定理,可以求出相應的線段的長,轉化為點的坐標,進而求出k的值【解答】解:過點C、D作CEx軸,DFx軸,垂足為E、F,ABCD是菱形,ABBCCDDA,易證ADFBCE,點A(4,0),D(1,4),DFCE4,OF1,AFOAOF3,在RtADF中,AD,OEEFOF514,C(4,4)k4416故答案為:16【點評】本題主要考查反比例函數圖象上點的坐標特征,綜合利用菱形的性質、全等三角形、直角三角形勾股定理,以及反比例函數圖象的性質;把點的坐標與線段的長度相互轉化也是解決問題重要方法15(3分)如圖,在ABC中,BAC90,ABAC10cm,點D為ABC內一點,BAD15,AD6cm,連接BD,將ABD繞點A按逆時針方向旋轉,使AB與AC重合,點D的對應點為點E,連接DE,DE交AC于點F,則CF的長為(102)cm【考點】KO:含30度角的直角三角形;KW:等腰直角三角形;R2:旋轉的性質菁優網版權所有【分析】過點A作AGDE于點G,由旋轉的性質推出AEDADG45,AFD60,利用銳角三角函數分別求出AG,GF,AF的長,即可求出CFACAF102【解答】解:過點A作AGDE于點G,由旋轉知:ADAE,DAE90,CAEBAD15,AEDADG45,在AEF中,AFDAED+CAE60,在RtADG中,AGDG3,在RtAFG中,GF,AF2FG2,CFACAF102,故答案為:102【點評】本題考查了旋轉的性質,等腰直角三角形的性質,解直角三角形等,解題的關鍵是能夠通過作適當的輔助線構造特殊的直角三角形,通過解直角三角形來解決問題三、解答題(本大題共8個小題,共75分,解答應寫出文字說明,證明過程或演算步驟)16(10分)(1)計算:+()23tan60+()0(2)解方程組:【考點】2C:實數的運算;6E:零指數冪;6F:負整數指數冪;98:解二元一次方程組;T5:特殊角的三角函數值菁優網版權所有【分析】(1)先根據二次根式的性質,特殊角的三角函數,0次冪進行計算,再合并同類二次根式;(2)用加減法進行解答便可【解答】解:(1)原式3+43+15;(2)+得,4x8,x2,把x2代入得,62y8,y1,【點評】本題是解答題的基本計算題,主要考查了實數的計算,解二元一次方程組,是基礎題,要求100%得分,不能有失誤17(7分)已知:如圖,點B,D在線段AE上,ADBE,ACEF,CF求證:BCDF【考點】KD:全等三角形的判定與性質菁優網版權所有【分析】由已知得出ABED,由平行線的性質得出AE,由AAS證明ABCEDF,即可得出結論【解答】證明:ADBE,ADBDBEBD,ABED,ACEF,AE,在ABC和EDF中,ABCEDF(AAS),BCDF【點評】本題考查了全等三角形的判定與性質、平行線的性質;熟練掌握平行線的性質,證明三角形全等是解題的關鍵18(9分)中華人民共和國第二屆青年運動會(簡稱二青會)將于2019年8月在山西舉行太原市作為主賽區,將承擔多項賽事,現正從某高校的甲、乙兩班分別招募10人作為頒獎禮儀志愿者,同學們踴躍報名,甲、乙兩班各報了20人,現已對他們進行了基本素質測評,滿分10分各班按測評成績從高分到低分的順序各錄用10人,對這次基本素質測評中甲、乙兩班學生的成績繪制了如圖所示的統計圖請解答下列問題:(1)甲班的小華和乙班的小麗基本素質測評成績都為7分,請你分別判斷小華,小麗能否被錄用(只寫判斷結果,不必寫理由)(2)請你對甲、乙兩班各被錄用的10名志愿者的成績作出評價(從“眾數”,“中位數”,或“平均數”中的一個方面評價即可)(3)甲、乙兩班被錄用的每一位志愿者都將通過抽取卡片的方式決定去以下四個場館中的兩個場館進行頒獎禮儀服務,四個場館分別為:太原學院足球場,太原市沙灘排球場,山西省射擊射箭訓練基地,太原水上運動中心,這四個場館分別用字母A,B,C,D表示現把分別印有A,B,C,D的四張卡片(除字母外,其余都相同)背面朝上,洗勻放好志愿者小玲從中隨機抽取一張(不放回),再從中隨機抽取一張,請你用列表或畫樹狀圖的方法求小玲抽到的兩張卡片恰好是“A”和“B”的概率【考點】W1:算術平均數;W4:中位數;W5:眾數;X6:列表法與樹狀圖法菁優網版權所有【分析】(1)判斷小華和小麗在各自班級的名次即可得出答案;(2)分別得出甲乙兩班的眾數、中位數和平均數,再判斷大小即可得;(3)畫樹狀圖列出所有等可能結果,從中找到符合條件的結果數,再根據概率公式計算可得【解答】解:(1)小華在甲班是第11名,不能錄用;小麗在乙班是第10名,可以錄用;(2)從眾數來看,甲乙兩班各被錄用的10名志愿者的眾數分別為8分、10分,說明甲班被錄用的10名志愿者中8分最多,乙班被錄用的10名志愿者中10分最多;從中位數來看,甲乙兩班被錄用的10名志愿者成績的中位數分別為9分、8.5分,說明甲班被錄用的10名志愿者成績的中位數大于乙班被錄用的10名志愿者成績的中位數;從平均數看,甲乙兩班被錄用的10名志愿者成績的平均數分別為8.9分、8.7分,說明甲班被錄用的10名志愿者成績的平均數大于乙班被錄用的10名志愿者成績的平均數(3)畫樹狀圖如下:由樹狀圖知,共有12種等可能結果,其中抽到的兩張卡片恰好是“A”和“B”的有2種結果,所以抽到的兩張卡片恰好是“A”和“B”的概率為【點評】本題考查讀頻數分布直方圖的能力和利用統計圖獲取信息的能力;利用統計圖獲取信息時,必須認真觀察、分析、研究統計圖,才能作出正確的判斷和解決問題19(8分)某游泳館推出了兩種收費方式方式一:顧客先購買會員卡,每張會員卡200元,僅限本人一年內使用,憑卡游泳,每次游泳再付費30元方式二:顧客不購買會員卡,每次游泳付費40元設小亮在一年內來此游泳館的次數為x次,選擇方式一的總費用為y1(元),選擇方式二的總費用為y2(元)(1)請分別寫出y1,y2與x之間的函數表達式(2)小亮一年內在此游泳館游泳的次數x在什么范圍時,選擇方式一比方式二省錢【考點】FH:一次函數的應用菁優網版權所有【分析】(1)根據題意列出函數關系式即可;(2)根據(1)中的函數關系式列不等式即可得到結論【解答】解:(1)當游泳次數為x時,方式一費用為:y130x+200,方式二的費用為:y240x;(2)由y1y2得:30x+20040x,解得x20時,當x20時,選擇方式一比方式二省錢【點評】本題考查一次函數的應用、一元一次不等式的應用,解答本題的關鍵是明確題意,找出所求問題需要的條件20(9分)某“綜合與實踐”小組開展了測量本校旗桿高度的實踐活動他們制訂了測量方案,并利用課余時間完成了實地測量他們在該旗桿底部所在的平地上,選取兩個不同測點,分別測量了該旗桿頂端的仰角以及這兩個測點之間的距離為了減小測量誤差,小組在測量仰角的度數以及兩個測點之間的距離時,都分別測量了兩次并取它們的平均值作為測量結果,測量數據如下表(不完整) 課題測量旗桿的高度成員組長:xxx 組員:xxx,xxx,xxx測量工具測量角度的儀器,皮尺等測量示意圖說明:線段GH表示學校旗桿,測量角度的儀器的高度ACBD1.5m,測點A,B與H在同一條水平直線上,A,B之間的距離可以直接測得,且點G,H,A,B,C,D都在同一豎直平面內,點C,D,E在同一條直線上,點E在GH 上測量數據測量項目第一次第二次平均值GCE的度數25.625.825.7GDE的度數31.230.831A,B之間的距離5.4m5.6m任務一:兩次測量A,B之間的距離的平均值是5.5m任務二:根據以上測量結果,請你幫助該“綜合與實踐”小組求出學校旗桿GH的高度(參考數據:sin25.70.43,cos25.70.90,tan25.70.48,sin310.52,cos310.86,tan310.60)任務三:該“綜合與實踐”小組在制定方案時,討論過“利用物體在陽光下的影子測量旗桿的高度”的方案,但未被采納你認為其原因可能是什么?(寫出一條即可)【考點】TA:解直角三角形的應用仰角俯角問題;U5:平行投影菁優網版權所有【分析】任務一:根據矩形的性質得到EHAC1.5,CDAB5.5;任務二:設ECxm,解直角三角形即可得到結論;任務三:根據題意得到沒有太陽光,或旗桿底部不可能達到等(答案不唯一)【解答】解:任務一:由題意可得,四邊形ACDB,四邊形ADEH是矩形,EHAC1.5,CDAB5.5,故答案為:5.5;任務二:設ECxm,在RtDEG中,DEC90,GDE31,tan31,DE,在RtCEG中,CEG90,GCE25.7,tan25.7,CE,CDCEDE,5.5,x13.2,GHCE+EH13.2+1.514.7,答:旗桿GH的高度為14.7米;任務三:沒有太陽光,或旗桿底部不可能達到【點評】本題考查的是解直角三角形的應用仰角俯角問題,掌握仰角俯角的概念、熟記銳角三角函數的定義是解題的關鍵21(8分)閱讀以下材料,并按要求完成相應的任務:萊昂哈德歐拉(LeonhardEuler)是瑞士數學家,在數學上經常見到以他的名字命名的重要常數,公式和定理,下面就是歐拉發現的一個定理:在ABC中,R和r分別為外接圓和內切圓的半徑,O和I分別為其中外心和內心,則OI2R22Rr如圖1,O和I分別是ABC的外接圓和內切圓,I與AB相切分于點F,設O的半徑為R,I的半徑為r,外心O(三角形三邊垂直平分線的交點)與內心I(三角形三條角平分線的交點)之間的距離OId,則有d2R22Rr下面是該定理的證明過程(部分):延長AI交O于點D,過點I作O的直徑MN,連接DM,ANDN,DMINAI(同弧所對的圓周角相等)MDIANI,IAIDIMIN,如圖2,在圖1(隱去MD,AN)的基礎上作O的直徑DE,連接BE,BD,BI,IFDE是O的直徑,所以DBE90I與AB相切于點F,所以AFI90,DBEIFABADE(同弧所對的圓周角相等),AIFEDB,IABDDEIF任務:(1)觀察發現:IMR+d,INRd(用含R,d的代數式表示);(2)請判斷BD和ID的數量關系,并說明理由(3)請觀察式子和式子,并利用任務(1),(2)的結論,按照上面的證明思路,完成該定理證明的剩余部分;(4)應用:若ABC的外接圓的半徑為5cm,內切圓的半徑為2cm,則ABC的外心與內心之間的距離為cm【考點】MR:圓的綜合題菁優網版權所有【分析】(1)直接觀察可得;(2)BDID,只要證明BIDDBI,由三角形內心性質和圓周角性質即可得證;(3)應用(1)(2)結論即可;(4)直接代入計算【解答】解:(1)O、I、N三點共線,OI+INONINONOIRd故答案為:Rd;(2)BDID理由如下:如圖3,過點I作O直徑MN,連接AI交O于D,連接MD,BI,BD,點I是ABC的內心BADCAD,CBIABIDBCCAD,BIDBAD+ABI,DBIDBC+CBIBIDDBIBDID(3)由(2)知:BDIDIAIDDEIFDEIFIMIN2Rr(R+d)(Rd)R2d22Rrd2R22Rr(4)由(3)知:d2R22Rr;將R5,r2代入得:d2522525,d0d故答案為:【點評】本題是圓綜合題,主要考查了三角形外接圓、外心和內切圓、內心,圓周角性質,角平分線定義,三角形外角性質等22(11分)綜合與實踐動手操作:第一步:如圖1,正方形紙片ABCD沿對角線AC所在的直線折疊,展開鋪平在沿過點C的直線折疊,使點B,點D都落在對角線AC上此時,點B與點D重合,記為點N,且點E,點N,點F三點在同一條直線上,折痕分別為CE,CF如圖2第二步:再沿AC所在的直線折疊,ACE與ACF重合,得到圖3第三步:在圖3的基礎上繼續折疊,使點C與點F重合,如圖4,展開鋪平,連接EF,FG,GM,ME如圖5,圖中的虛線為折痕問題解決:(1)在圖5中,BEC的度數是67.5,的值是(2)在圖5中,請判斷四邊形EMGF的形狀,并說明理由;(3)在不增加字母的條件下,請你以圖中5中的字母表示的點為頂點,動手畫出一個菱形(正方形除外),并寫出這個菱形:菱形EMCH或菱形FGCH【考點】SO:相似形綜合題菁優網版權所有【分析】(1)由折疊的性質得BEEN,AEAF,CEBCEN,BACCAD,由正方形性質得EAF90,推出AEFAFE45,得出BEN135,BEC67.5,證得AEN是等腰直角三角形,得出AEEN,即可得出結果;(2)由正方形性質得BBCDD90,由折疊的性質得BCEECAACFFCD,CMCG,BECNECNFCDFC,得出BCE
- 關 鍵 詞:
- 2019 山西省 中考 數學試卷
 叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。
叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。 關于本文



 譯林版五年級上英語Project 1 參考教案.doc
譯林版五年級上英語Project 1 參考教案.doc  譯林版五年級上英語Unit 1 第2課時教學設計.doc
譯林版五年級上英語Unit 1 第2課時教學設計.doc  譯林版五年級上英語Project 2 參考教案.docx
譯林版五年級上英語Project 2 參考教案.docx  譯林版五年級上英語Unit 1 第3課時教學設計.doc
譯林版五年級上英語Unit 1 第3課時教學設計.doc  譯林版五年級上英語Unit 1 第4課時教學設計.doc
譯林版五年級上英語Unit 1 第4課時教學設計.doc  譯林版五年級上英語Unit 1 第1課時教學設計.doc
譯林版五年級上英語Unit 1 第1課時教學設計.doc  譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx  譯林版五年級上冊英語知識點總結+梳理.docx
譯林版五年級上冊英語知識點總結+梳理.docx  譯林版五年級上英語Unit 7 第1課時參考教案.docx
譯林版五年級上英語Unit 7 第1課時參考教案.docx  譯林版五年級上英語Unit 6 第3課時參考教案.docx
譯林版五年級上英語Unit 6 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第3課時參考教案.docx
譯林版五年級上英語Unit 4 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第1課時參考教案.docx
譯林版五年級上英語Unit 4 第1課時參考教案.docx  譯林版五年級上英語Unit 2 第3課時教學設計.doc
譯林版五年級上英語Unit 2 第3課時教學設計.doc  譯林版五年級上英語Unit 2 第1課時教學設計.doc
譯林版五年級上英語Unit 2 第1課時教學設計.doc  譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx  譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx  贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc
贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc 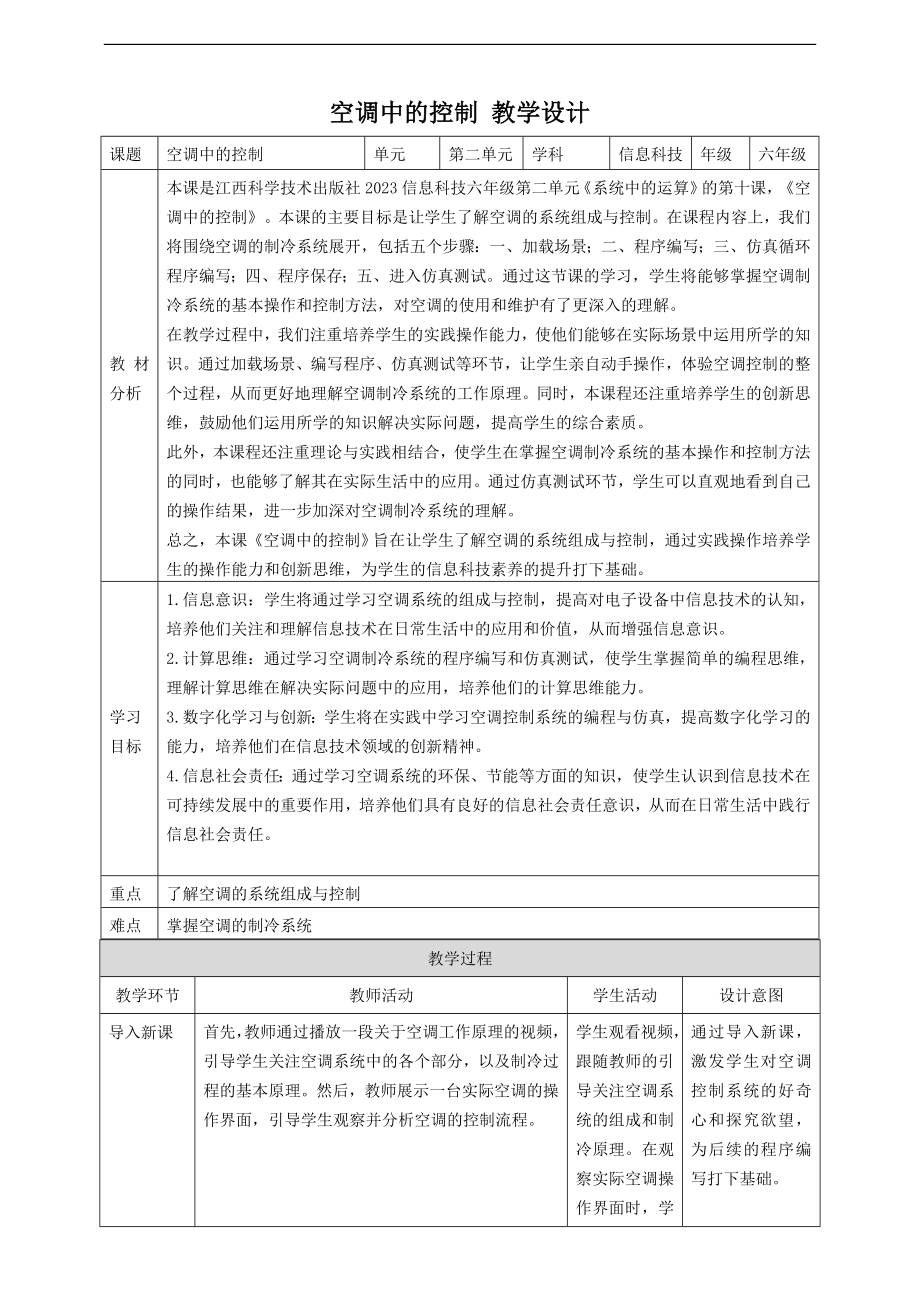 贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar
贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar 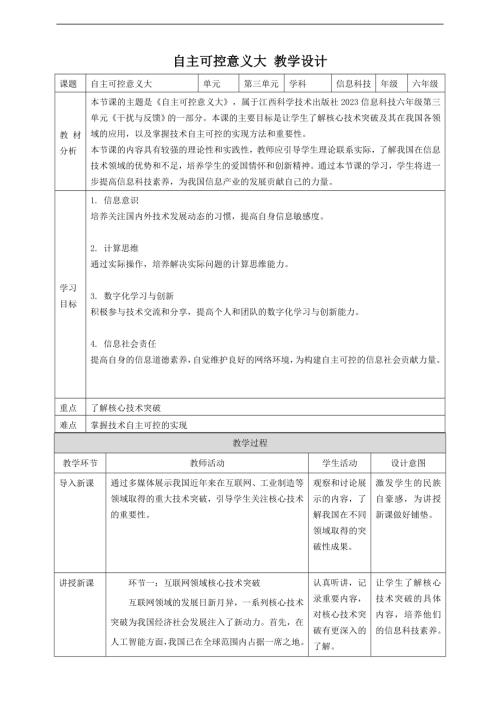 贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc
贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc  贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx 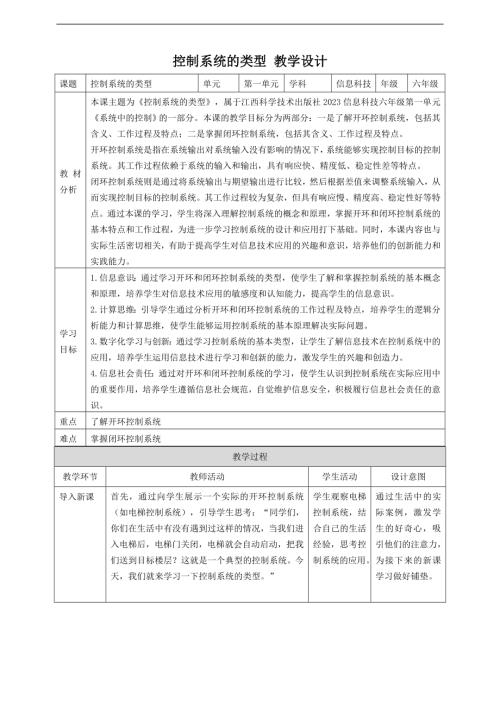 贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc
贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc  贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc
贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc  贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx
贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx 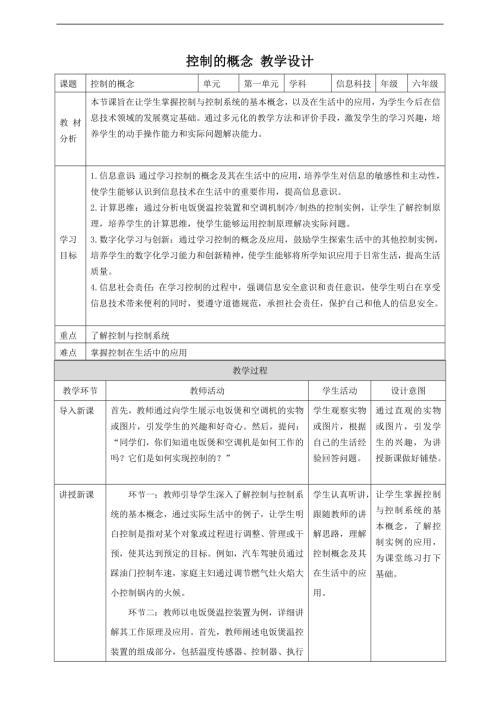 贛科版六年級下冊信息科技第1課 控制的概念 教案.doc
贛科版六年級下冊信息科技第1課 控制的概念 教案.doc  贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx
贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx  贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc  贛科版六年級下冊信息科技第12課 反饋概述 教案.doc
贛科版六年級下冊信息科技第12課 反饋概述 教案.doc  贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx  贛科版六年級下冊信息科技第2課 控制的分類 教案.doc
贛科版六年級下冊信息科技第2課 控制的分類 教案.doc  贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx
贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx  贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx 


