 初中數學九年級下冊第27章圓27.1圓的認識作業設計新版華東師大版.docx
初中數學九年級下冊第27章圓27.1圓的認識作業設計新版華東師大版.docx
27.1圓的認識第1課時1.下列結論正確的是()A.弦是直徑B.弧是半圓C.半圓是弧D.過圓心的線段是直徑2.如圖,在半圓的直徑上作4個正三角形,若半圓周長為C1,4個正三角形的周長和為C2,則C1和C2的大小關系是()A.C1C2B.C12OAB B.AOC=2OABC.AOC2OAB D.不能確定5.如圖,弦AC,BD相交于E,并且AB=BC=CD,BEC=110,則ACD的度數是 .6.如圖,AB是O的直徑,已知AB=2,C,D是O上的兩點,且BC+BD=23AB,M是AB上一點,則MC+MD的最小值是 .7.如圖所示,在O中,AB,CD為直徑,判斷AD與BC的位置關系.8.如圖,已知AB為O的直徑,點C為半圓ACB上的動點(不與A,B兩點重合),過點C作弦CDAB,OCD的平分線交圓于點P,則點P的位置有何規律?請證明你的結論.參考答案1.B 2.D 3.C 4.B 5. 75 6. 3 7. 解:ADBC.理由:因為AB,CD為O的直徑,所以OA=OD=OC=OB.又AOD=BOC,所以AODBOC.所以A=B.所以ADBC,即AD與BC的位置關系為平行.8. 解:點P為半圓ADB的中點.理由如下:連結OP,如圖,因為OCD的平分線交圓于點P,所以PCD=PCO,因為OC=OP,所以PCO=OPC,所以PCD=OPC,所以OPCD,因為CDAB,所以OPAB,所以PA=PB,即點P為半圓ADB的中點.第3課時1.如圖,在O中,AB=AC,AOB=40,則ADC的度數是()A.40B.30C.20D.152.如圖,BC是O的直徑,A是O上一點,OAC=32,則B的度數是()A.58B.60C.64D.683.如圖,點A,B,C,D都在O上,且四邊形OABC是平行四邊形,則D的度數為()A.45B.60C.75 D.不能確定4.如圖,在半徑為5的O中,弦AB=6,點C是優弧ACB上一點(不與A,B重合),則cos C的值為()A.43 B.34 C.35 D.455.如圖,C過原點,且與兩坐標軸分別交于點A,點B,點A的坐標為(0,3),M是第三象限內C上一點,BMO=120,則C的半徑為()A.6B.5C.3D.2236. AB為半圓O的直徑,現將一塊等腰直角三角板如圖放置,銳角頂點P在半圓上,斜邊過點B,一條直角邊交該半圓于點Q.若AB=2,則線段BQ的長為 .7.如圖,圓心角AOB=30,弦CAOB,延長CO與圓交于點D,則BOD= .8.如圖,已知O的內接四邊形ABCD兩組對邊的延長線分別交于點E,F,若E+F=70,則A的度數是 .9.如圖,已知A,B,C,D是O上的四點,延長DC,AB相交于點E,若BC=BE.求證:ADE是等腰三角形.10.如圖所示,O的直徑AB為10 cm,弦AC為6 cm,ACB的平分線交O于D,求BC,AD,BD的長.11. A,B是圓O上的兩點,AOB=60,C是圓O上不與A,B重合的任一點,求ACB的度數是多少?12.如圖,在O中,AB是直徑,CD是弦(不過圓心),ABCD.(1)E是優弧CAD上一點(不與C,D重合),求證:CED=COB;(2)點E在劣弧CD上(不與C,D重合)時,CED與COB有什么數量關系?請證明你的結論.參考答案1.C 2.A 3.B 4.D 5.C 6. 2 7. 30 8. 559. 證明:因為A,D,C,B四點共圓,所以A+BCD=180,因為BCD+BCE=180,所以A=BCE,因為BC=BE,所以BCE=E,所以A=E,所以AD=DE,即ADE是等腰三角形.10. 解:因為AB是直徑,所以ACB=ADB=90,在RtABC中,AB2=AC2+BC2,AB=10 cm,AC=6 cm,所以BC2=AB2-AC2=102-62=64,所以BC=64=8(cm),又CD平分ACB,所以ACD=BCD,所以AD=DB,所以AD=BD,又在RtABD中,AD2+BD2=AB2,所以AD2+BD2=102,所以AD=BD=1002=52(cm).11. 解:分兩種情況:(1)當C點在劣弧AB上時,如圖所示,A,B是圓O上兩點,AOB=60,所以弧AB的度數為60,優弧ADB的度數為300,所以ACB=150.(2)當點C在優弧ADB上時,ACB=12AOB=30.綜上所述ACB為30或150.12. (1)證明:如圖所示,連結OD.因為AB是直徑,ABCD,所以BC=BD,所以COB=DOB=12COD.又因為CED=12COD,所以CED=COB.(2)解:CED與COB的數量關系是CED+COB=180.理由:因為CED=12COD,CED=180-CED,由(1)知,CED=COB,所以CED+COB=180
- 關 鍵 詞:
- 初中 數學 九年級 下冊 27 章圓 27.1 認識 作業 設計 新版 華東師大
 叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。
叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。 關于本文
相關資源
 華師大版九下數學27.1.2 第1課時 圓的對稱性 課件.ppt
華師大版九下數學27.1.2 第1課時 圓的對稱性 課件.ppt  華師大版九下數學26.3 第3課時 利用兩個函數的圖象求方程(組)和不等式的解 課件.ppt
華師大版九下數學26.3 第3課時 利用兩個函數的圖象求方程(組)和不等式的解 課件.ppt  華師大版九下數學第26章 小結與復習 課件.ppt
華師大版九下數學第26章 小結與復習 課件.ppt  華師大版九下數學27.1.2 第2課時 垂徑定理 課件.ppt
華師大版九下數學27.1.2 第2課時 垂徑定理 課件.ppt  華師大版九下數學26.2.1 二次函數y=ax2的圖象與性質 課件.ppt
華師大版九下數學26.2.1 二次函數y=ax2的圖象與性質 課件.ppt  華師大版九下數學27.1.1 圓的基本元素 課件.ppt
華師大版九下數學27.1.1 圓的基本元素 課件.ppt  華師大版九下數學26.2.2 第1課時二次函數y=ax2+k的圖象與性質 課件.ppt
華師大版九下數學26.2.2 第1課時二次函數y=ax2+k的圖象與性質 課件.ppt  華師大版九下數學26.1 二次函數 課件.ppt
華師大版九下數學26.1 二次函數 課件.ppt  華師大版九下數學26.2.2 第3課時二次函數y=a(x-h)2+k的圖象與性質 課件.ppt
華師大版九下數學26.2.2 第3課時二次函數y=a(x-h)2+k的圖象與性質 課件.ppt  華師大版九下數學26.2.2 第2課時二次函數y=a(x-h)2的圖象與性質 課件.ppt
華師大版九下數學26.2.2 第2課時二次函數y=a(x-h)2的圖象與性質 課件.ppt 


 譯林版五年級上英語Project 1 參考教案.doc
譯林版五年級上英語Project 1 參考教案.doc  譯林版五年級上英語Unit 1 第2課時教學設計.doc
譯林版五年級上英語Unit 1 第2課時教學設計.doc  譯林版五年級上英語Project 2 參考教案.docx
譯林版五年級上英語Project 2 參考教案.docx  譯林版五年級上英語Unit 1 第3課時教學設計.doc
譯林版五年級上英語Unit 1 第3課時教學設計.doc  譯林版五年級上英語Unit 1 第4課時教學設計.doc
譯林版五年級上英語Unit 1 第4課時教學設計.doc  譯林版五年級上英語Unit 1 第1課時教學設計.doc
譯林版五年級上英語Unit 1 第1課時教學設計.doc  譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx  譯林版五年級上冊英語知識點總結+梳理.docx
譯林版五年級上冊英語知識點總結+梳理.docx  譯林版五年級上英語Unit 7 第1課時參考教案.docx
譯林版五年級上英語Unit 7 第1課時參考教案.docx  譯林版五年級上英語Unit 6 第3課時參考教案.docx
譯林版五年級上英語Unit 6 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第3課時參考教案.docx
譯林版五年級上英語Unit 4 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第1課時參考教案.docx
譯林版五年級上英語Unit 4 第1課時參考教案.docx  譯林版五年級上英語Unit 2 第3課時教學設計.doc
譯林版五年級上英語Unit 2 第3課時教學設計.doc  譯林版五年級上英語Unit 2 第1課時教學設計.doc
譯林版五年級上英語Unit 2 第1課時教學設計.doc  譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx  譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx  贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc
贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc 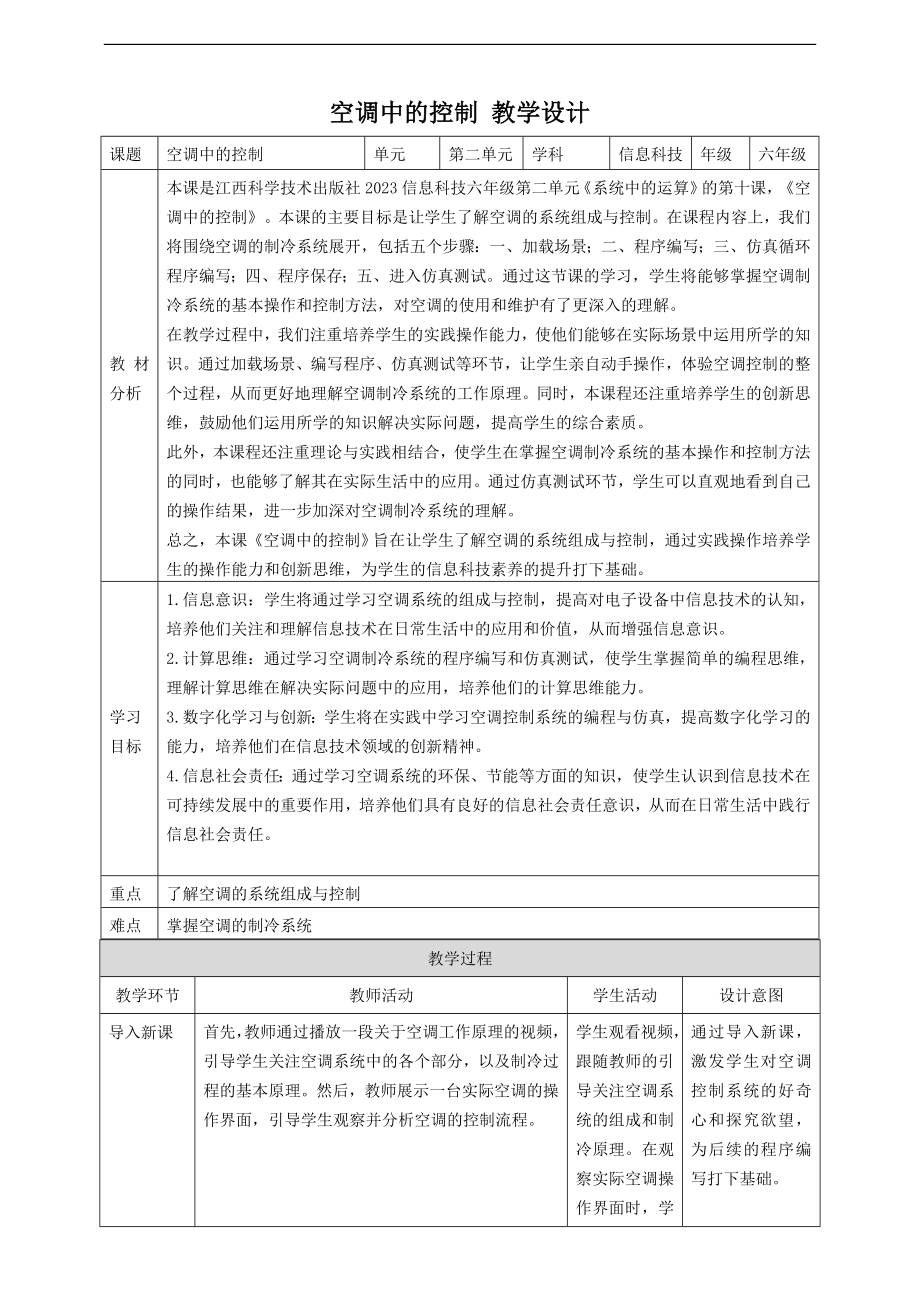 贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar
贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar 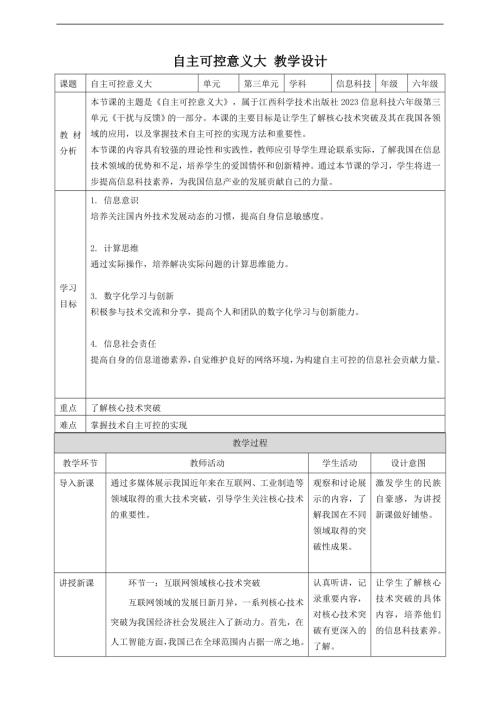 贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc
贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc  贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx 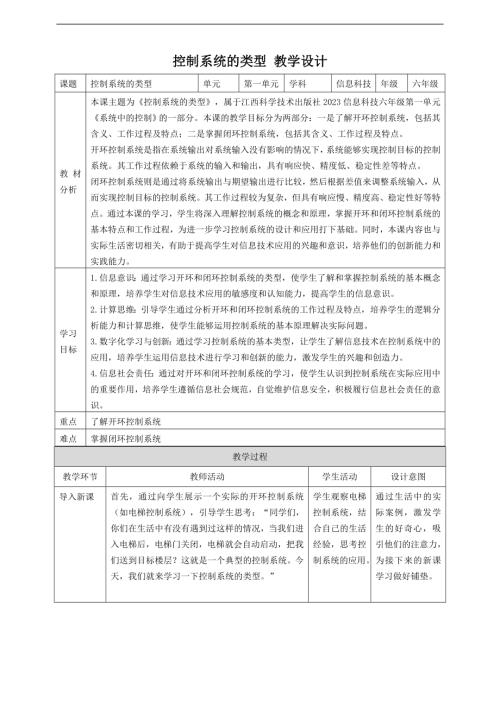 贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc
贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc  贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc
贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc  贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx
贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx 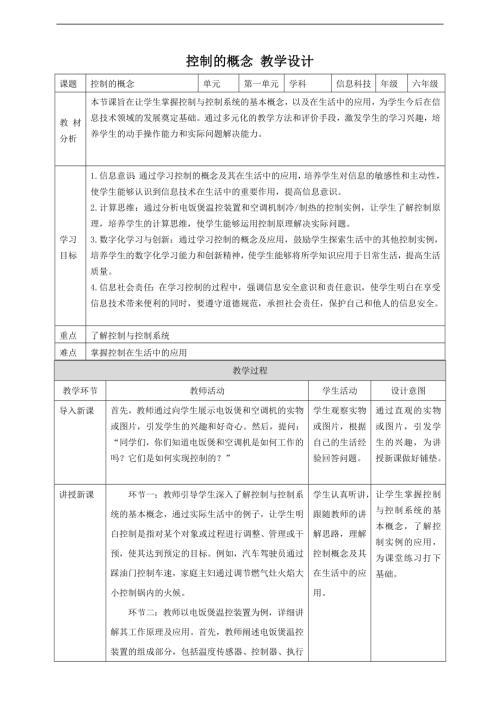 贛科版六年級下冊信息科技第1課 控制的概念 教案.doc
贛科版六年級下冊信息科技第1課 控制的概念 教案.doc  贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx
贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx  贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc  贛科版六年級下冊信息科技第12課 反饋概述 教案.doc
贛科版六年級下冊信息科技第12課 反饋概述 教案.doc  贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx  贛科版六年級下冊信息科技第2課 控制的分類 教案.doc
贛科版六年級下冊信息科技第2課 控制的分類 教案.doc  贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx
贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx  贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx 

