 初中數學九年級下冊第2章直線與圓的位置關系2.3三角形的內切圓教學課件新版浙教版.pptx
初中數學九年級下冊第2章直線與圓的位置關系2.3三角形的內切圓教學課件新版浙教版.pptx
教學課件數學九年級下冊浙教版第2章直線與圓的位置關系2.3三角形的內切圓學習目標:1、了解三角形的內切圓、三角形的內心、圓的外切三角形的概念。2、會利用基本作圖作三角形的內切圓。3、了解三角形內心的性質,并會進行有關的計算。1任意作一個ABC,如果在ABC內作圓,使其與兩邊OA、OB相切,滿足上述條件的圓是否可以作出?如果可以作,能作多少個?所作出的圓的圓心O的位置有什么特征?為什么?圓心O在ABC的平分線上。能作無數個2任意作一個ABC,在ABC內作圓,使其與各邊都相切,滿足上述條件的圓是否可以作出?如果可以作,能作多少個?所作出的圓的圓心O的位置有什么特征?為什么?圓心O在ABC與ACB的兩個角的角平分線的交點上。圖2ABC作出三個內角的平分線,三條內角平分線相交于一點,這點就是圓心,過圓心作一邊的垂線,垂線段的長就是半徑。OCABD3如何確定與三角形三邊都相切的圓的圓心位置與半徑的長?三角形與圓的位置關系與三角形各邊都相切的圓叫做三角形的內切圓.這個三角形叫做圓的外切三角形.內切圓的圓心叫做三角形的內心.三角形的內心是三角形三條角平分線的交點。老師提示:三角形的邊與圓的位置關系稱為切.ABC下列各圖,是三角形的內切圓的是()1.已知ABC的三邊長分別為a,b,c,它的內切圓半徑為r,你會求ABC的面積嗎?2.已知RtABC的兩直角邊分別為a,b,你會求它的內切圓半徑嗎?O.ABCabcrr=a+b-c2rO已知:如圖,在RtABC中,C=90,邊BC、AC、AB的長分別為a、b、c,求其內切圓O的半徑長.EDrra-ra-rb-r+a-r=cb-rFb-r1.本節課從實際問題入手,探索得出三角形內切圓的作法.2.通過類比三角形的外接圓與圓的內接三角形概念得出三角形的內切圓、圓的外切三角形概念.3.學習時要明確“接”和“切”的含義、弄清“內心”與“外心”的區別.4.利用三角形內心的性質解題時,要注意整體思想和化整為零思想的運用.課堂小結
- 關 鍵 詞:
- 初中 數學 九年級 下冊 直線 位置 關系 2.3 三角形 內切圓 教學 課件 新版 浙教版
 叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。
叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。 關于本文
相關資源
 初中數學九年級下冊第2章直線與圓的位置關系2.2切線長定理教學課件新版浙教版.pptx
初中數學九年級下冊第2章直線與圓的位置關系2.2切線長定理教學課件新版浙教版.pptx  初中數學九年級下冊第1章解直角三角形1.1銳角三角函數教學課件新版浙教版.pptx
初中數學九年級下冊第1章解直角三角形1.1銳角三角函數教學課件新版浙教版.pptx  初中數學九年級下冊第3章三視圖與表面展開圖3.1投影教學課件新版浙教版.pptx
初中數學九年級下冊第3章三視圖與表面展開圖3.1投影教學課件新版浙教版.pptx  初中數學九年級下冊第3章三視圖與表面展開圖3.3由三視圖描述幾何體教學課件新版浙教版.pptx
初中數學九年級下冊第3章三視圖與表面展開圖3.3由三視圖描述幾何體教學課件新版浙教版.pptx  初中數學九年級下冊第1章解直角三角形1.3解直角三角形教學課件新版浙教版.pptx
初中數學九年級下冊第1章解直角三角形1.3解直角三角形教學課件新版浙教版.pptx  初中數學九年級下冊第3章三視圖與表面展開圖3.2簡單幾何體的三視圖教學課件新版浙教版.pptx
初中數學九年級下冊第3章三視圖與表面展開圖3.2簡單幾何體的三視圖教學課件新版浙教版.pptx  初中數學九年級下冊第2章直線與圓的位置關系2.1直線與圓的位置關系教學課件新版浙教版.pptx
初中數學九年級下冊第2章直線與圓的位置關系2.1直線與圓的位置關系教學課件新版浙教版.pptx  初中數學九年級下冊第1章解直角三角形1.2銳角三角函數的計算教學課件新版浙教版.pptx
初中數學九年級下冊第1章解直角三角形1.2銳角三角函數的計算教學課件新版浙教版.pptx  初中數學九年級下冊第3章三視圖與表面展開圖3.4簡單幾何體的表面展開圖教學課件新版浙教版.pptx
初中數學九年級下冊第3章三視圖與表面展開圖3.4簡單幾何體的表面展開圖教學課件新版浙教版.pptx 


 譯林版五年級上英語Project 1 參考教案.doc
譯林版五年級上英語Project 1 參考教案.doc  譯林版五年級上英語Unit 1 第2課時教學設計.doc
譯林版五年級上英語Unit 1 第2課時教學設計.doc  譯林版五年級上英語Project 2 參考教案.docx
譯林版五年級上英語Project 2 參考教案.docx  譯林版五年級上英語Unit 1 第3課時教學設計.doc
譯林版五年級上英語Unit 1 第3課時教學設計.doc  譯林版五年級上英語Unit 1 第4課時教學設計.doc
譯林版五年級上英語Unit 1 第4課時教學設計.doc  譯林版五年級上英語Unit 1 第1課時教學設計.doc
譯林版五年級上英語Unit 1 第1課時教學設計.doc  譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx  譯林版五年級上冊英語知識點總結+梳理.docx
譯林版五年級上冊英語知識點總結+梳理.docx  譯林版五年級上英語Unit 7 第1課時參考教案.docx
譯林版五年級上英語Unit 7 第1課時參考教案.docx  譯林版五年級上英語Unit 6 第3課時參考教案.docx
譯林版五年級上英語Unit 6 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第3課時參考教案.docx
譯林版五年級上英語Unit 4 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第1課時參考教案.docx
譯林版五年級上英語Unit 4 第1課時參考教案.docx  譯林版五年級上英語Unit 2 第3課時教學設計.doc
譯林版五年級上英語Unit 2 第3課時教學設計.doc  譯林版五年級上英語Unit 2 第1課時教學設計.doc
譯林版五年級上英語Unit 2 第1課時教學設計.doc  譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx  譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx 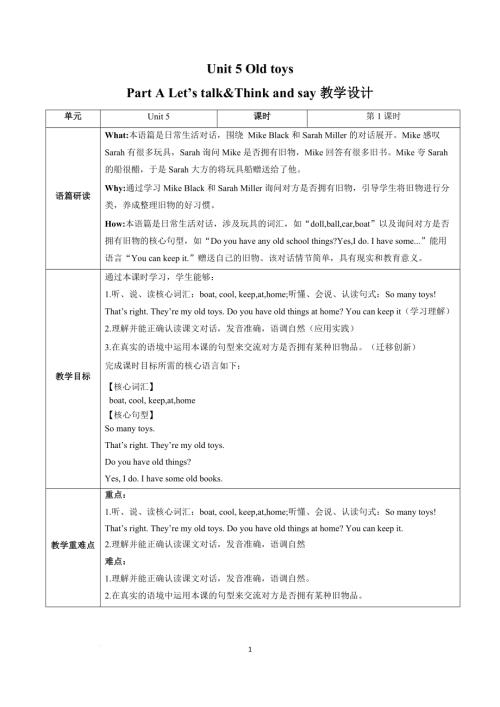 人教PEP版三年級下英語Unit 5 第1課時 (教學設計) Part A Let’s talk&Think and say.docx
人教PEP版三年級下英語Unit 5 第1課時 (教學設計) Part A Let’s talk&Think and say.docx  人教PEP版三年級下英語Unit 4 第6課時(教學設計)Part B Read and write&Part C.docx
人教PEP版三年級下英語Unit 4 第6課時(教學設計)Part B Read and write&Part C.docx  人教PEP版三年級下英語Unit 5 第2課時 (教學設計) Part A Let's learn & Listen and chant.docx
人教PEP版三年級下英語Unit 5 第2課時 (教學設計) Part A Let's learn & Listen and chant.docx 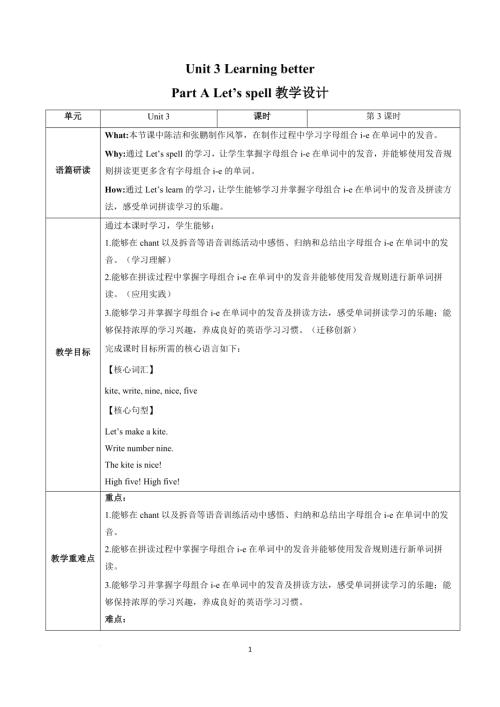 人教PEP版三年級下英語Unit 3 第3課時 (教學設計) Part A Let's spell-.docx
人教PEP版三年級下英語Unit 3 第3課時 (教學設計) Part A Let's spell-.docx  人教PEP版三年級下英語Unit 3 第2課時 (教學設計) Part A Let's learn&Listen and do.docx
人教PEP版三年級下英語Unit 3 第2課時 (教學設計) Part A Let's learn&Listen and do.docx  人教PEP版三年級下英語Unit 4 第5課時(教學設計)Part B Let's learn&Listen and chant.docx
人教PEP版三年級下英語Unit 4 第5課時(教學設計)Part B Let's learn&Listen and chant.docx  人教PEP版三年級下英語Unit 3 第4課時 (教學設計) Part B Let's talk&Play a guessing game.docx
人教PEP版三年級下英語Unit 3 第4課時 (教學設計) Part B Let's talk&Play a guessing game.docx 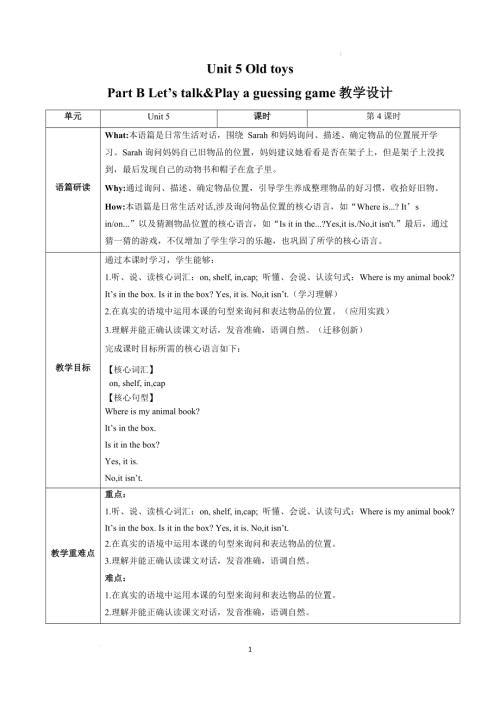 人教PEP版三年級下英語Unit 5 第4課時 (教學設計) Part B Let’s talk&Play a guessing game.docx
人教PEP版三年級下英語Unit 5 第4課時 (教學設計) Part B Let’s talk&Play a guessing game.docx 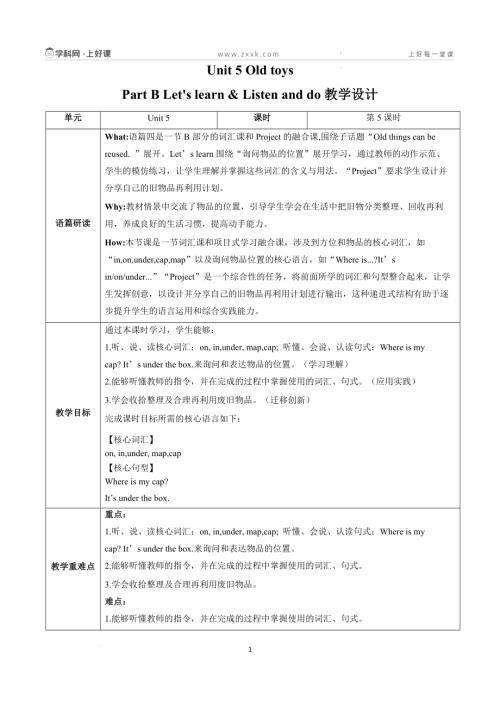 人教PEP版三年級下英語Unit 5 第5課時 (教學設計) Part B Let's learn & Listen and do.docx
人教PEP版三年級下英語Unit 5 第5課時 (教學設計) Part B Let's learn & Listen and do.docx  人教PEP版三年級下英語Unit 1 第5課時(教學設計)Part B Let's learn&Listen and do.docx
人教PEP版三年級下英語Unit 1 第5課時(教學設計)Part B Let's learn&Listen and do.docx  人教PEP版三年級下英語Unit 1 第4課時(教學設計)Part B Let's talk&Choose and say.docx
人教PEP版三年級下英語Unit 1 第4課時(教學設計)Part B Let's talk&Choose and say.docx  人教PEP版三年級下英語Unit 3 第1課時 (教學設計) Part A Let's talk&Ask and answer.docx
人教PEP版三年級下英語Unit 3 第1課時 (教學設計) Part A Let's talk&Ask and answer.docx  人教PEP版三年級下英語Unit 3 第6課時 (教學設計) Part B Read and write&Part C.docx
人教PEP版三年級下英語Unit 3 第6課時 (教學設計) Part B Read and write&Part C.docx  人教PEP版三年級下英語Unit 1 第6課時(教學設計)Part B Read and write&Part C.docx
人教PEP版三年級下英語Unit 1 第6課時(教學設計)Part B Read and write&Part C.docx  人教PEP版三年級下英語Unit 5 第6課時 (教學設計) Part B Read and write & Part C.docx
人教PEP版三年級下英語Unit 5 第6課時 (教學設計) Part B Read and write & Part C.docx 

