 湘教版八年級下冊數學1.2 第3課時 勾股定理的逆定理1 練習題含答案.doc
湘教版八年級下冊數學1.2 第3課時 勾股定理的逆定理1 練習題含答案.doc
1.2 直角三角形的性質和判定()第3課時 勾股定理的逆定理一、選擇題1.下列各組數中,是勾股數的是( )A. 14,36,39B. 8,24,25C. 8,15,17D. 10,20,262.下列定理中,有逆定理的個數是( )有兩邊相等的三角形是等腰三角形;若三角形的三邊長a,b,c滿足a2+b2=c2,則該三角形是直角三角形;全等三角形的對應角相等;若a=b, a2 =b2. A. 1個 B. 2個 C. 3個 D. 4個來源:學科網ZXXK3下面各選項給出的是三角形中各邊的長度的平方比,其中不是直角三角形的是( )A.112B.134C.92526D.251441694.(易錯題)在ABC中,A,B,C的對邊分別是 a,b,c,那么下面不能判定ABC是直角三角形的是( )A.B=C-AB.a2 = (b+c) (b-c)C.A:B:C=5 :4 :3來源:學科網ZXXKD.a : b : c=5 : 4 : 35.五根小木棒,其長度分別為7,15,20,24,25,現將它們擺成各選項所示的兩個直角三角形,其中正確的是( )二、填空題6在兩個命題中,如果第一個命題的題設是第二個命題的結論,而第一個命題的結論是第二個命題的題設,那么這兩個命題叫做____________;如果把其中一個命題叫做原命題,那么另一個命題叫做它的____________7在ABC中,a、b、c分別是A、B、C的對邊,若a2b2c2,則c為____________;若a2b2c2,則c為____________;若a2b2c2,則c為____________8若一個三角形的三邊長分別為1、a、8(其中a為正整數),則以a2、a、a2為邊的三角形的面積為______9ABC的兩邊a,b分別為5,12,另一邊c為奇數,且abc是3的倍數,則c應為______,此三角形為______10.如圖,D為ABC的邊BC上一點,已知 AB = 13,AD = 12,AC =15,BD=5,則BC的長為 .三、解答題11.寫出下列命題的逆命題,并判斷這些逆命題是否成立.(1)如果a=0,那么 ab=0;(2)如果x=4,那么x2=16;(3)面積相等的三角形是全等三角形;(4)如果三角形有一個內角是鈍角,那么其余兩個角是銳角;(5)在一個三角形中,等角對等邊.12已知:如圖,四邊形ABCD中,ABBC,AB1,BC2,CD2,AD3,求四邊形ABCD的面積13在B港有甲、乙兩艘漁船,若甲船沿北偏東60方向以每小時8海里的速度前進,乙船沿南偏東某個角度以每小時15海里的速度前進,2小時后,甲船到M島,乙船到P島,兩島相距34海里,你知道乙船是沿哪個方向航行的嗎?14已知a、b、c是ABC的三邊,且a2c2b2c2a4b4,試判斷三角形的形狀15.(教材習題變式)如圖所示,在四邊形 ABCD 中,B= 90,AB=4,BC=3,CD=12,AD=13,求四邊形ABCD的面積.16.觀察下列各組勾股數的組成特點,你能求出第7組勾股數a,b,c各是多少嗎?第n組呢?第 1 組:3=2X1+1,4=2X1X(1+1),5=2X1X(1 + 1)+1;第 2 組:5=2X2+1,12=2X2X(2+1),13=2X2X(2+1) + 1;第 3 組:7=2X3+1,24=2X3X(3+1),25=2X3X(3+1) + 1;第 4 組:9=2X4+1,40=2X4X(4+1),41=2X4X(4+1) + 1;第 7 組:a,b,c.來源:學|科|網參考答案1. C 解析 142+362=1492.392=15211492,A項不是勾股數;82+242=640,252=625640,B項不是勾股數;82+152=289,172=289,C項是勾股數;102+202=500,262=676500,D項不是勾股數.點撥:一組數是勾股數,必須符合兩個條件:(1)三個數必須是正整數.(2)兩個較小數的平方和等于最大數的平方.2. B 解析 的逆命題是“等腰三角形有兩邊相等”,是真命題;的逆命題是“若直角三角形的兩條直角邊長分別為a,b,斜邊長為c,則三邊長a,b,c滿足a2+b2=c2”,是真命題;對應角相等的兩個三角形不一定全等;若a2=b2,則a與b不一定相等,所以的逆命題是假命題,沒有逆等理.3C 4. C 解析 A選項,B=C-A,A+B+C=A+C-A+C=180,C=90,ABC是直角三角形;B選項,a2=(b+c)(b-c),即a2+c2=b2,ABC為直角三角形;C選項,A:B:C=5:4:3,則最大角A=180=75,則ABC為銳角三角形;D選項,a:b:c=5:4:3,則a2=b2+c2,則ABC為直角三角形,故選C.來源:學科網5. C 解析 因為72+242=252,152+202=252,所以用長度為7,24,25和15,20,25的小木棒能分別擺成直角三角形,故選C.6互逆命題,逆命題7銳角;直角;鈍角 824提示:7a9,a8 913,直角三角形提示:7c1710. 14 解析 由AD2+BD2=AB2可知ABC為直角三角形,則AD為ABC的BC邊上的高,在RtACD中,CD2=AC2-AD2=152-122=81,所以CD=9,BC=BD+CD=5+9=14.11. 解:(1)的逆命題是如果ab=0,那么a=0.不成立.(2)的逆命題是如果x2=16,那么x=4.不成立.(3)的逆命題是全等三角形的面積相等.成立.(4)的逆命題是如果三角形有兩個內角是銳角,那么另一個內角是鈍角.不成立.(5)的逆命題是在一個三角形中,等邊對等角.成立.點撥:要確定一個命題的逆命題,只要將原命題的題設與結論互換即可.1213南偏東3014等腰三角形或直角三角形提示:原式可變形為(a2b2)(a2b2c2)015. 解:如圖所示,連接AC.B=90,ABC是直角三角形.依據勾股定理的AC2=AB2+BC2=42+32=25=52,AC=5.在ACD中,AD2=132=169,CD2+AC2=122+52=169,AD2=AC2+CD2.ACD是直角三角形,ACD=90.S四邊形ABCD=SABC+SACD=ABBC+ACCD=43+512=6+30=36.四邊形ABCD的面積為36.方法:要求不規則四邊形ABCD的面積,可把四邊形分割成幾個三角形,這是常用的方法.此題是先利用勾股定理求出AC的長,再利用勾股定理的逆定理判斷ACD為直角三角形,即原四邊形ABCD可分割成兩個直角三角形.來源:學_科_網Z_X_X_K16. 分析:觀察已知勾股數的特點,找出規律.解:第7組:a=27+1=15,b=27(7+1)=112,c=27(7+1)+1=113.第n組:a=2n+1,b=2n(n+1),c=2n(n+1)+1
- 關 鍵 詞:
- 湘教版八年級下冊數學1.2 第3課時 勾股定理的逆定理1 練習題含答案 湘教版八 年級 下冊 數學 1.2 課時 勾股定理 逆定理 練習題 答案
 叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。
叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。 關于本文
相關資源
 湘教版八年級下冊數學電子課本(教材全冊電子書).pdf
湘教版八年級下冊數學電子課本(教材全冊電子書).pdf  湘教版八年級下冊數學2.1《多邊形的概念及內角和》課件(湖南部優).ppt
湘教版八年級下冊數學2.1《多邊形的概念及內角和》課件(湖南部優).ppt  湘教版八年級下冊數學2.1《多邊形的外角和》課件(重慶部級優課).pptx
湘教版八年級下冊數學2.1《多邊形的外角和》課件(重慶部級優課).pptx  湘教版八年級下冊數學1.2勾股定理(第1課時)教案(湖南縣級優課).doc
湘教版八年級下冊數學1.2勾股定理(第1課時)教案(湖南縣級優課).doc  湘教版八年級下冊數學1.2勾股定理(第1課時)課件(湖南部級優課).pptx
湘教版八年級下冊數學1.2勾股定理(第1課時)課件(湖南部級優課).pptx  湘教版八年級下冊數學2.1《多邊形的概念及內角和》教案(湖南部優).docx
湘教版八年級下冊數學2.1《多邊形的概念及內角和》教案(湖南部優).docx  湘教版八年級下冊數學2.1《多邊形的概念及內角和》課件(湖南部級優課).pptx
湘教版八年級下冊數學2.1《多邊形的概念及內角和》課件(湖南部級優課).pptx  湘教版八年級下冊數學2.1《多邊形的外角和》教案(黑龍江縣級優課).doc
湘教版八年級下冊數學2.1《多邊形的外角和》教案(黑龍江縣級優課).doc  湘教版八年級下冊數學2.1《多邊形的概念及內角和》教案(湖南部級優課).doc
湘教版八年級下冊數學2.1《多邊形的概念及內角和》教案(湖南部級優課).doc  湘教版八年級下冊數學2.1《多邊形的外角和》課件(黑龍江縣級優課).pptx
湘教版八年級下冊數學2.1《多邊形的外角和》課件(黑龍江縣級優課).pptx 


 譯林版五年級上英語Project 1 參考教案.doc
譯林版五年級上英語Project 1 參考教案.doc  譯林版五年級上英語Unit 1 第2課時教學設計.doc
譯林版五年級上英語Unit 1 第2課時教學設計.doc  譯林版五年級上英語Project 2 參考教案.docx
譯林版五年級上英語Project 2 參考教案.docx  譯林版五年級上英語Unit 1 第3課時教學設計.doc
譯林版五年級上英語Unit 1 第3課時教學設計.doc  譯林版五年級上英語Unit 1 第4課時教學設計.doc
譯林版五年級上英語Unit 1 第4課時教學設計.doc  譯林版五年級上英語Unit 1 第1課時教學設計.doc
譯林版五年級上英語Unit 1 第1課時教學設計.doc  譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx  譯林版五年級上冊英語知識點總結+梳理.docx
譯林版五年級上冊英語知識點總結+梳理.docx  譯林版五年級上英語Unit 7 第1課時參考教案.docx
譯林版五年級上英語Unit 7 第1課時參考教案.docx  譯林版五年級上英語Unit 6 第3課時參考教案.docx
譯林版五年級上英語Unit 6 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第3課時參考教案.docx
譯林版五年級上英語Unit 4 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第1課時參考教案.docx
譯林版五年級上英語Unit 4 第1課時參考教案.docx  譯林版五年級上英語Unit 2 第3課時教學設計.doc
譯林版五年級上英語Unit 2 第3課時教學設計.doc  譯林版五年級上英語Unit 2 第1課時教學設計.doc
譯林版五年級上英語Unit 2 第1課時教學設計.doc  譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx  譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx  贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc
贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc  贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar
贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar  贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc
贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc  贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx  贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc
贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc  贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc
贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc  贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx
贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx  贛科版六年級下冊信息科技第1課 控制的概念 教案.doc
贛科版六年級下冊信息科技第1課 控制的概念 教案.doc  贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx
贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx 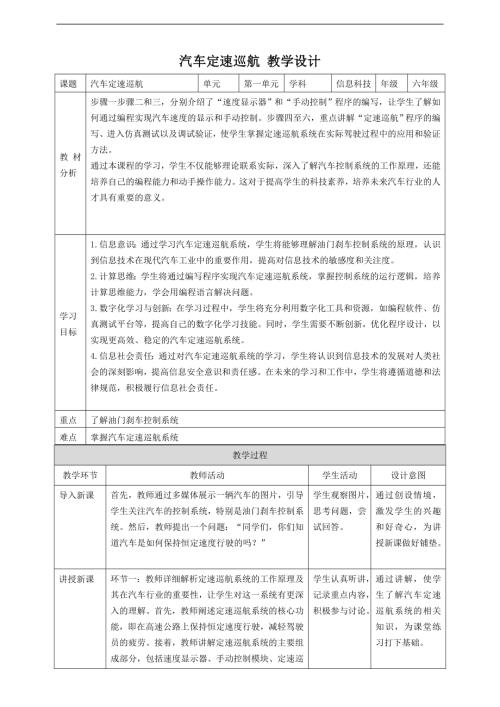 贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc  贛科版六年級下冊信息科技第12課 反饋概述 教案.doc
贛科版六年級下冊信息科技第12課 反饋概述 教案.doc  贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx 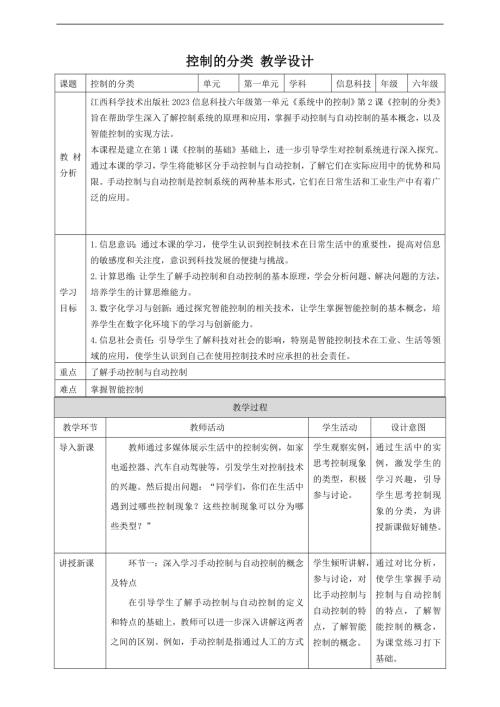 贛科版六年級下冊信息科技第2課 控制的分類 教案.doc
贛科版六年級下冊信息科技第2課 控制的分類 教案.doc  贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx
贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx  贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx 

