 人教版九年級下冊數學26.1.1反比例函數 教案.docx
人教版九年級下冊數學26.1.1反比例函數 教案.docx
第二十六章 反比例函數26.11反比例函數一、教學目標1理解并掌握反比例函數的概念。2能判定一個給定的函數是否為反比例函數,并會用待定系數法求函數的解析式。3能根據實際問題中的條件確定反比例函數的解析式。二、教學重難點重點:理解反比例函數的概念.難點:確定反比例函數的解析式,理解反比例與反比例函數的區別。 三、教學過程【新課導入】復習導入1.什么是函數?2.我們學過的函數有哪些?它們的解析式分別是什么? 【新知探究】(一)觀察分析,引入新知。問題1:京滬線鐵路全程為1463km,某次列車的平均速度v(單位:km/h)隨此次列車的全程運動時間t(單位:h)的變化而變化。師問:平均速度v與時間t存在著怎樣的關系?這三者中,誰是常量,誰是變量?兩個變量間具有函數關系嗎?誰變化了誰也跟著變化?你能寫出列車的平均速度v與行駛時間t的函數關系式嗎?問題2:下列問題中,變量間具有函數關系嗎?如果有,請寫出他們的函數關系式,并思考它們的關系式具有什么特點?(1) 某住宅小區要種植一塊面積為1000m2的矩形草坪,草坪的長y(單位:m)隨寬x(單位:m)的變化而變化。 (2) 已知北京市的總面積為1.68104km2,人均占有面積S(單位:km2/人)隨全市總人口n(單位:人)的變化而變化。師問:在這兩個問題中,變量是什么?常量是什么?他們具有什么樣的函數關系式?請寫出它們的關系式。以上三個問題中的解析式都具有什么共同特點?(二)歸納總結,建立模型。 1.反比例函數的定義:一般地,形如 (k為常數,k0)的函數,叫做反比例函數。其中x是自變量,y是函數。自變量x的取值范圍是不等于0的一切實數。2 反比例函數的三種表示方法: (k為常數,k0) (k為常數,k0) (k為常數,k0)(三)辨析概念,靈活運用。例1:下列哪些式子表示y是x的反比例函數?若是反比例函數,請說出k的值。(1) __________________ (2) y=5x ____________________(3) __________________ (4) ____________________(5) __________________ (6) ____________________(7) _________________ (8) ____________________例2:已知關于x的函數是反比例函數,求m的值。分析:根據反比例函數的定義,且(四)分析例題,培養能力。例3:已知y是x的反比例函數,并且當x=2時,y=6(1) 寫出y關于x的函數解析式。(2) 當x=4時,求y的值。分析:因為y是x的反比例函數,所以可以設,把x=2和y=6代入,求出k的值。(學生充分理解了反比例函數的概念,也會用待定系數法求函數的解析式。)例3變式:已知y-2與x+3成反比例,且當x=2時,y=-3(1) 求y與x的函數關系式。(2) 當y=7時,x的值是多少?解:(1)設,將x=2,y=-3代入得: 解得:k=-25(2)把y=7代入中得x=-8 難點:把y-2與x+3看成一個整體,明確反比例與反比例函數的區別與聯系,進一步加深對反比例函數概念的理解。【課堂小結】1.反比例函數的定義:一般地,形如 (k為常數,k0)的函數,叫做反比例函數。其中x是自變量,y是函數。自變量x的取值范圍是不等于0的一切實數。2 反比例函數的三種表示方法: (k為常數,k0) (k為常數,k0) (k為常數,k0)【課堂訓練】1.在下列函數中,y是x的反比例函數的是( )A B C D 2. 若函數為反比例函數,則m的值是( )A 1 B 0 C D -13.如果直角三角形的面積一定,那么下列關于這個直角三角形的關系的說法中,正確的是( )A 兩條直角邊成正比例 B 兩條直角邊成反比例C 一條直角邊與斜邊成正比例 D 一條直角邊與斜邊成反比例4.若是關于x的反比例函數,則m的值為__________5.已知y與x+2成反比例,并且當x=2是y=-6(1) 請寫出y關于x的函數關系式。(2) 當x=4時,求y的值。(3) 當y=4時,求x的值。【布置作業】書第3頁練習1,習題26.1第1,2題。【教學反思】通過學習學生更深刻理解反比例函數的概念,會運用反比例函數的概念解決一些問題。在應用中要重點區分反比例與反比例函數。學生更加熟練用待定系數法解函數的解析式
- 關 鍵 詞:
- 人教版九年級下冊數學26.1.1反比例函數 教案 人教版 九年級 下冊 數學 26.1 反比例 函數
 叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。
叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。 關于本文
相關資源
 人教版九年級下冊數學全冊教學設計教案(總229頁).docx
人教版九年級下冊數學全冊教學設計教案(總229頁).docx  人教版九年級下冊數學28.1銳角三角函數 第二課時 課件.pptx
人教版九年級下冊數學28.1銳角三角函數 第二課時 課件.pptx  人教版九年級下冊數學教學課件ppt(全冊合輯打包).rar
人教版九年級下冊數學教學課件ppt(全冊合輯打包).rar  人教版九年級下冊數學28.1銳角三角函數 第一課時 課件.pptx
人教版九年級下冊數學28.1銳角三角函數 第一課時 課件.pptx  人教版九年級下冊數學26.2 實際問題與反比例函數課件.pptx
人教版九年級下冊數學26.2 實際問題與反比例函數課件.pptx  人教版九年級下冊數學28.2 解直角三角形及其應用 第二課時課件.pptx
人教版九年級下冊數學28.2 解直角三角形及其應用 第二課時課件.pptx  人教版九年級下冊數學26.1.2 反比例函數的圖像和性質 第二課時 課件.pptx
人教版九年級下冊數學26.1.2 反比例函數的圖像和性質 第二課時 課件.pptx  人教版九年級下冊數學29.2 三視圖 第二課時 課件.pptx
人教版九年級下冊數學29.2 三視圖 第二課時 課件.pptx  人教版九年級下冊數學29.3 課題學習 課件.pptx
人教版九年級下冊數學29.3 課題學習 課件.pptx  人教版九年級下冊數學29.2 三視圖 第一課時 課件.pptx
人教版九年級下冊數學29.2 三視圖 第一課時 課件.pptx 


 譯林版五年級上英語Project 1 參考教案.doc
譯林版五年級上英語Project 1 參考教案.doc  譯林版五年級上英語Unit 1 第2課時教學設計.doc
譯林版五年級上英語Unit 1 第2課時教學設計.doc  譯林版五年級上英語Project 2 參考教案.docx
譯林版五年級上英語Project 2 參考教案.docx  譯林版五年級上英語Unit 1 第3課時教學設計.doc
譯林版五年級上英語Unit 1 第3課時教學設計.doc  譯林版五年級上英語Unit 1 第4課時教學設計.doc
譯林版五年級上英語Unit 1 第4課時教學設計.doc  譯林版五年級上英語Unit 1 第1課時教學設計.doc
譯林版五年級上英語Unit 1 第1課時教學設計.doc  譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx  譯林版五年級上冊英語知識點總結+梳理.docx
譯林版五年級上冊英語知識點總結+梳理.docx  譯林版五年級上英語Unit 7 第1課時參考教案.docx
譯林版五年級上英語Unit 7 第1課時參考教案.docx  譯林版五年級上英語Unit 6 第3課時參考教案.docx
譯林版五年級上英語Unit 6 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第3課時參考教案.docx
譯林版五年級上英語Unit 4 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第1課時參考教案.docx
譯林版五年級上英語Unit 4 第1課時參考教案.docx  譯林版五年級上英語Unit 2 第3課時教學設計.doc
譯林版五年級上英語Unit 2 第3課時教學設計.doc  譯林版五年級上英語Unit 2 第1課時教學設計.doc
譯林版五年級上英語Unit 2 第1課時教學設計.doc  譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx  譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx  贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc
贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc 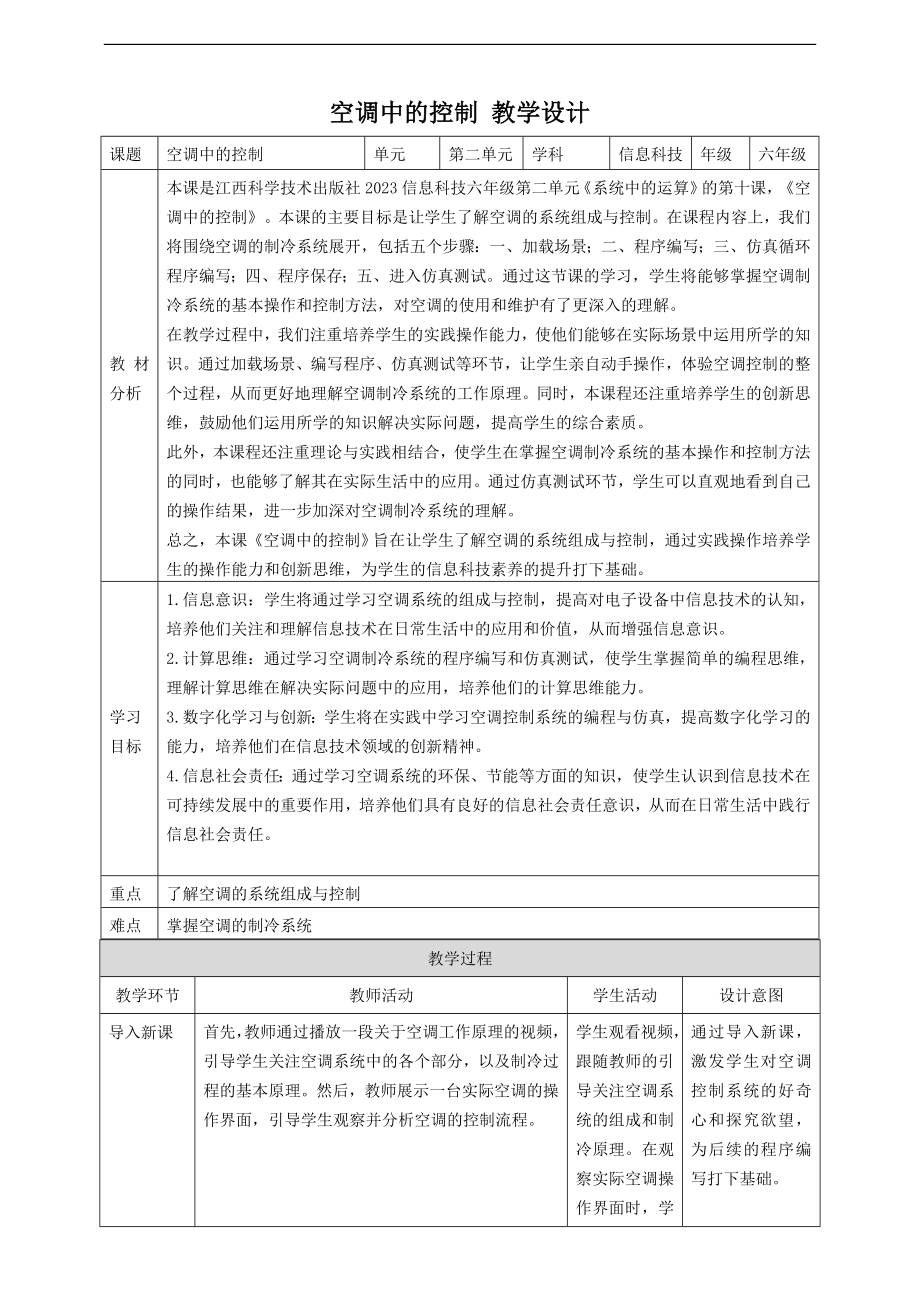 贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar
贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar 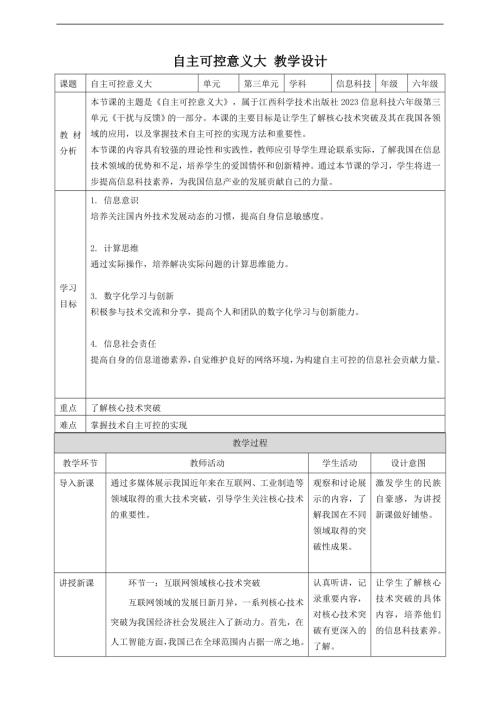 贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc
贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc  贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx 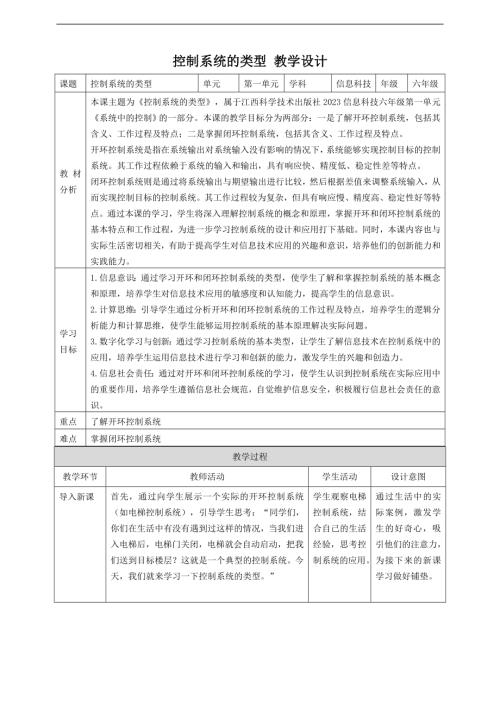 贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc
贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc  贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc
贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc  贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx
贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx 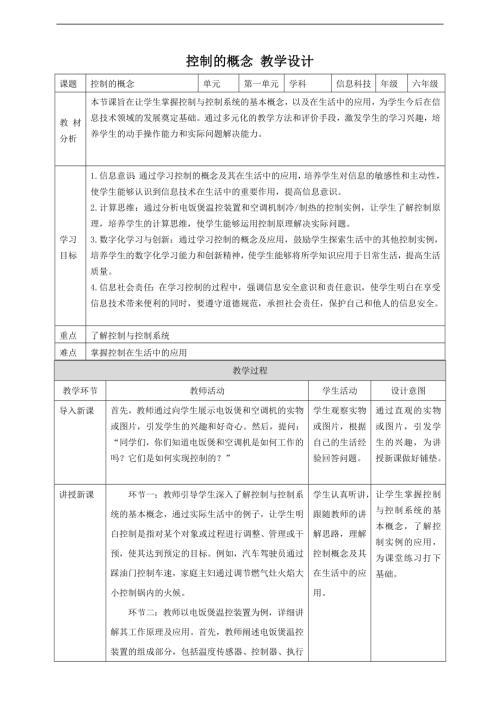 贛科版六年級下冊信息科技第1課 控制的概念 教案.doc
贛科版六年級下冊信息科技第1課 控制的概念 教案.doc  贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx
贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx  贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc  贛科版六年級下冊信息科技第12課 反饋概述 教案.doc
贛科版六年級下冊信息科技第12課 反饋概述 教案.doc  贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx  贛科版六年級下冊信息科技第2課 控制的分類 教案.doc
贛科版六年級下冊信息科技第2課 控制的分類 教案.doc  贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx
贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx  贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx 

