 人教版九下數學第26章第2課時 反比例函數的圖象和性質(2):不等式、最值 課件.pptx
人教版九下數學第26章第2課時 反比例函數的圖象和性質(2):不等式、最值 課件.pptx
第二十六章反比例函數,反比例函數的圖象和性質(2): 不等式、最值,1單個函數值的不等式問題(比較函數值大小)方法: (1)代入求值法;(2)圖象直觀法;(3)性質推導法 2單個函數的最值問題:定端點,定圖象,定結果 3兩個函數的函數值的不等式問題:找交點,分區間,判結果,(1)點(1,m),(2,n)在反比例函數y 的圖象上,則m________n; (2)在反比例函數y 的圖象上任取點A(x1,y1)和點B(x2,y2)如果0 x1x2,那么y1________y2.,(1)已知反比例函數y 的圖象上有兩點A(1,m),B(2,n),則m ________ n; (2)已知反比例函數y 的圖象上有兩個點(x1,y1),(x2,y2),其中x10 x2,則y1 ________ y2.,已知y是x的反比例函數,且x4時,y6. (1)寫出y與x之間的函數關系式; 解: y ; (2)如果自變量x的取值范圍為2x3.求y的取值范圍 解:8y12.,點A(2,1)在反比例函數y 的圖象上,若x4,結合圖象: (1)求y的取值范圍;,(2)求y的最值,如圖,在平面直角坐標系中,反比例函數y1 的圖象與一次函數y2kxb的圖象交于A,B兩點若y1y2,則x的取值范圍是() A1x3 Bx0或1x3 C0 x1 Dx3或0 x1,B,(2021宜春一模)如圖,直線y1x1與雙曲線y2 交于A(2,a),B(3,b)兩點,則當y1y2時,x的取值范圍是() Ax2 B2x0或x3 Cx2或0 x3 D2x3,C,一級 1對于反比例函數y ,當1x0時,y的取值范圍是() Ay6B6y0 C0y6Dy6,D,Ay2y3y1By2y1y3 Cy3y1y2 Dy3y2y1,C,二級 3已知反比例函數y ,則當x1時,函數值y的取值范圍是() Ay1B0y1 Cy2D0y2,D,4(2021中山市模擬)如圖,直線y1x1與雙曲線y2 交于A(2,m),B(3,n)兩點則當y1y2時,x的取值范圍是() Ax3或0 x2 B3x0或x2 Cx3或0 x2 D3x2,B,三級 5已知反比例函數y ,當1x2時,y的最小整數值是() A5 B6 C8 D10 6已知反比例函數y ,當y3時,自變量x的取值范圍是________________.,B,x2或x0,7(2021深圳模擬)如圖,直線y1axb(a0)與雙曲線y2 (k0)交于A、B兩點,與x軸交于點C,點A的縱坐標為6,點B的坐標為(3,2) (1)求直線和雙曲線的解析式; 解:直線的解析式為y12x4; 雙曲線的解析式為y2 ;,(2)求點C的坐標,并結合圖象直接寫出axb 0時,x的取值范圍 解:令y10,得x2, 點C的坐標為(2,0), 3x0或x1.,8.如圖,已知A(4,n),B(2,4)是一次函數y1kxb的圖象和反比例函數y2 的圖象的兩個交點,(1)求反比例函數和一次函數的解析式;,得m2(4)8,,解得n2,則A點坐標為(4,2), 把A(4,2),B(2,4)分別代入y1kxb. 所以一次函數的解析式為y1x2;,8.如圖,已知A(4,n),B(2,4)是一次函數y1kxb的圖象和反比例函數y2 的圖象的兩個交點,(2)直接寫出當y12.,本部分內容講解結束,按ESC鍵退出全屏播放
- 關 鍵 詞:
- 人教版九下數學第26章第2課時反比例函數的圖象和性質2:不等式、最值 課件 人教版九下 數學 26 課時 反比例 函數 圖象 性質 不等式
 叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。
叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。 關于本文
相關資源
 人教版九年級下冊數學全冊教學設計教案(總229頁).docx
人教版九年級下冊數學全冊教學設計教案(總229頁).docx  人教版九年級下冊數學28.1銳角三角函數 第二課時 課件.pptx
人教版九年級下冊數學28.1銳角三角函數 第二課時 課件.pptx  人教版九年級下冊數學教學課件ppt(全冊合輯打包).rar
人教版九年級下冊數學教學課件ppt(全冊合輯打包).rar  人教版九年級下冊數學28.1銳角三角函數 第一課時 課件.pptx
人教版九年級下冊數學28.1銳角三角函數 第一課時 課件.pptx  人教版九年級下冊數學26.2 實際問題與反比例函數課件.pptx
人教版九年級下冊數學26.2 實際問題與反比例函數課件.pptx  人教版九年級下冊數學28.2 解直角三角形及其應用 第二課時課件.pptx
人教版九年級下冊數學28.2 解直角三角形及其應用 第二課時課件.pptx  人教版九年級下冊數學26.1.2 反比例函數的圖像和性質 第二課時 課件.pptx
人教版九年級下冊數學26.1.2 反比例函數的圖像和性質 第二課時 課件.pptx  人教版九年級下冊數學29.2 三視圖 第二課時 課件.pptx
人教版九年級下冊數學29.2 三視圖 第二課時 課件.pptx  人教版九年級下冊數學29.3 課題學習 課件.pptx
人教版九年級下冊數學29.3 課題學習 課件.pptx  人教版九年級下冊數學29.2 三視圖 第一課時 課件.pptx
人教版九年級下冊數學29.2 三視圖 第一課時 課件.pptx 


 人教PEP六年級上冊英語Unit 1 Part ALet's learn &Make a map and talk課件.rar
人教PEP六年級上冊英語Unit 1 Part ALet's learn &Make a map and talk課件.rar  人教PEP版六年級上冊英語Unit6 Part ALet's try & Let's talk課件.rar
人教PEP版六年級上冊英語Unit6 Part ALet's try & Let's talk課件.rar  24新教材科普版三年級上英語Unit 12 Revision (2)課件.pptx
24新教材科普版三年級上英語Unit 12 Revision (2)課件.pptx  24新教材科普版小學英語三年級上冊-字母&四會單詞書寫練習.pdf
24新教材科普版小學英語三年級上冊-字母&四會單詞書寫練習.pdf  24新教材科普版三年級上英語Unit 8 My age (3)課件.pptx
24新教材科普版三年級上英語Unit 8 My age (3)課件.pptx  24新教材科普版小學英語三年級上冊課文翻譯文本.pdf
24新教材科普版小學英語三年級上冊課文翻譯文本.pdf  24新教材科普版三年級上英語Unit 12 Revision (1)課件.pptx
24新教材科普版三年級上英語Unit 12 Revision (1)課件.pptx  24新教材科普版三年級上英語Unit 10 My new friends (1)課件.pptx
24新教材科普版三年級上英語Unit 10 My new friends (1)課件.pptx  24新教材科普版三年級上英語Unit 11 Maths in everyday life (2)課件.pptx
24新教材科普版三年級上英語Unit 11 Maths in everyday life (2)課件.pptx  24新教材科普版三年級上英語Unit 9 My family (1)課件.pptx
24新教材科普版三年級上英語Unit 9 My family (1)課件.pptx  24新教材科普版三年級上英語Unit 9 My family (2)課件.pptx
24新教材科普版三年級上英語Unit 9 My family (2)課件.pptx  24新教材科普版三年級上英語Unit 11 Maths in everyday life (1)課件.pptx
24新教材科普版三年級上英語Unit 11 Maths in everyday life (1)課件.pptx  24新教材科普版三年級上英語Unit 5 Animals around us (2)課件.pptx
24新教材科普版三年級上英語Unit 5 Animals around us (2)課件.pptx  24新教材科普版三年級上英語Unit 10 My new friends (3)課件.pptx
24新教材科普版三年級上英語Unit 10 My new friends (3)課件.pptx  24新教材科普版三年級上英語Unit 8 My age (2)課件.pptx
24新教材科普版三年級上英語Unit 8 My age (2)課件.pptx  24新教材科普版三年級上英語Unit 9 My family (3)課件.pptx
24新教材科普版三年級上英語Unit 9 My family (3)課件.pptx  贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc
贛科版六年級下冊信息科技第10課 主題活動:空調中的控制 教案.doc 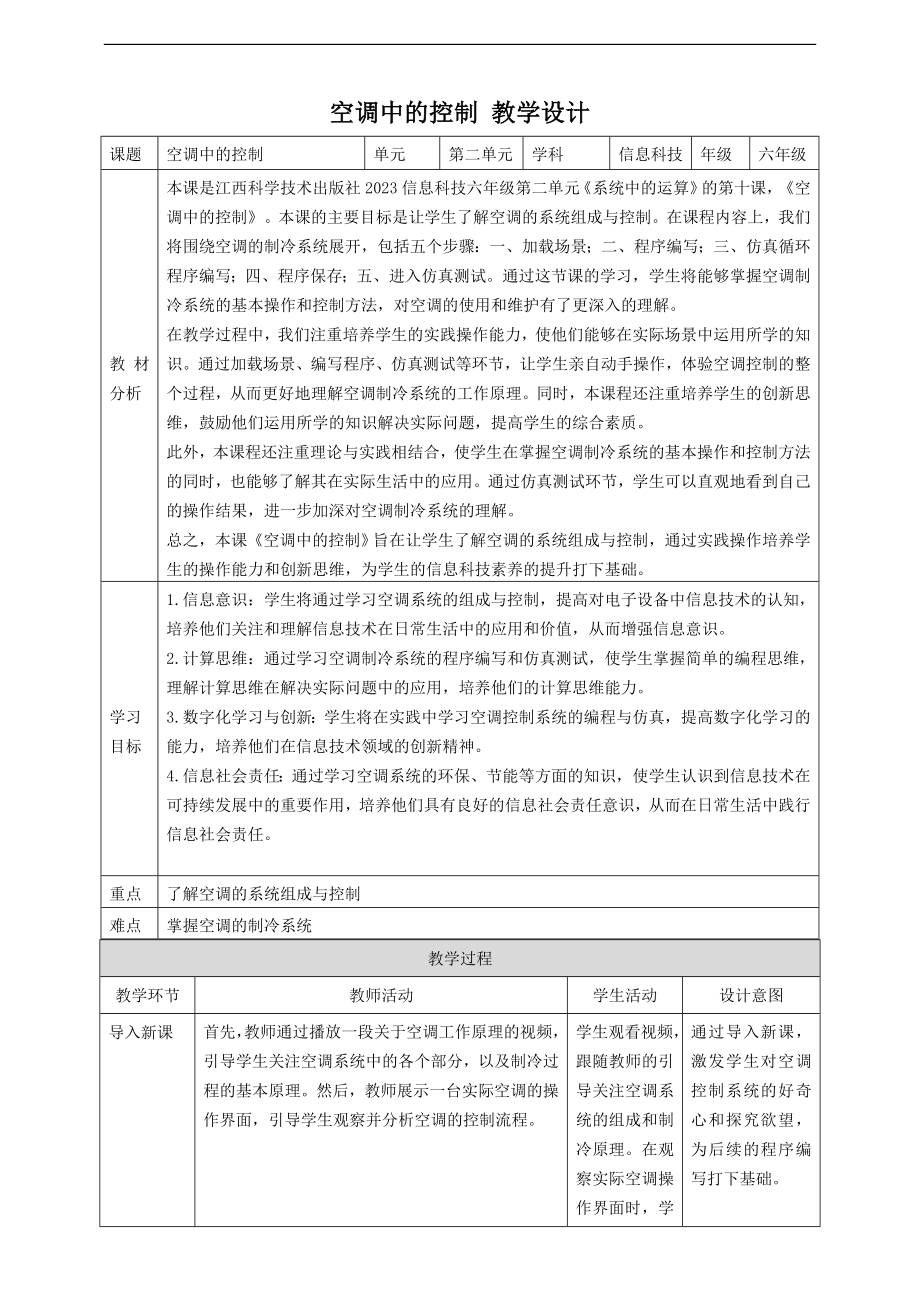 贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar
贛科版六年級下冊信息科技教案(全冊教學設計打包下載).rar 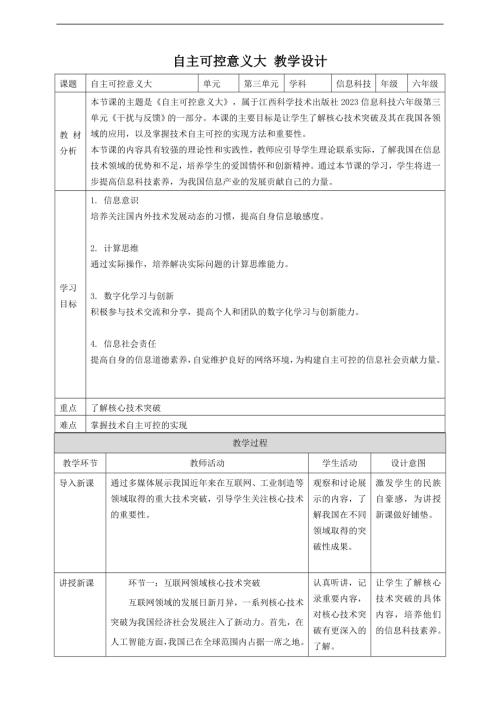 贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc
贛科版六年級下冊信息科技第14課 自主可控意義大 教案.doc  贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技15 跨學科主題:小型擴音系統 課件(共16張PPT) .pptx 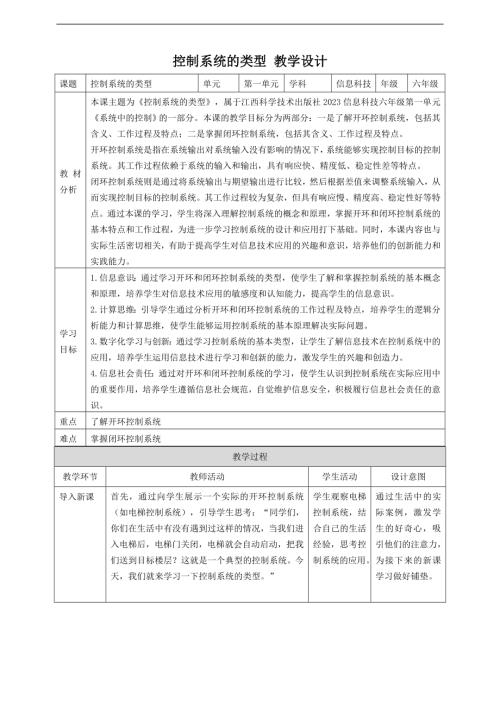 贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc
贛科版六年級下冊信息科技第4課 控制系統的類型 教案.doc  贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc
贛科版六年級下冊信息科技第11課 控制系統中的干擾 教案.doc  贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx
贛科版六年級下冊信息科技11控制系統中的干擾 課件(共22張PPT).pptx 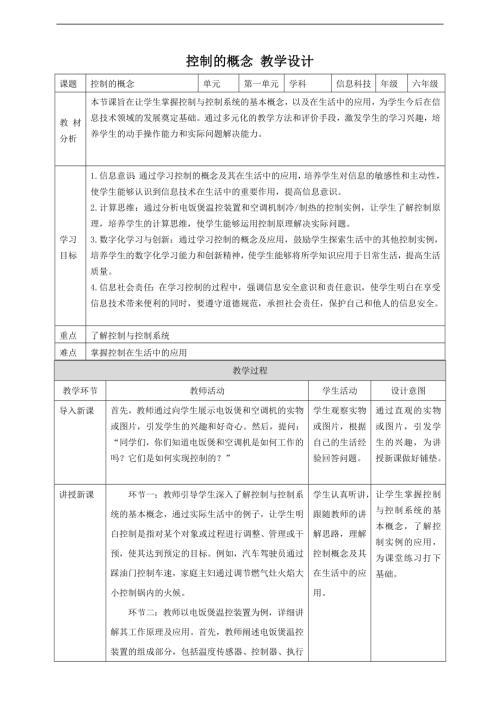 贛科版六年級下冊信息科技第1課 控制的概念 教案.doc
贛科版六年級下冊信息科技第1課 控制的概念 教案.doc  贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx
贛科版六年級下冊信息科技14 自主可控意義大 課件(共23張PPT) .pptx  贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 教案.doc  贛科版六年級下冊信息科技第12課 反饋概述 教案.doc
贛科版六年級下冊信息科技第12課 反饋概述 教案.doc  贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx
贛科版六年級下冊信息科技10 主題活動:空調中的控制 課件(共16張PPT) .pptx  贛科版六年級下冊信息科技第2課 控制的分類 教案.doc
贛科版六年級下冊信息科技第2課 控制的分類 教案.doc  贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx
贛科版六年級下冊信息科技13 反饋的類型 課件(共17張PPT) .pptx  贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx
贛科版六年級下冊信息科技第5課 主題活動:汽車定速巡航 課件(共15張PPT) .pptx 
